
【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系.
(一)发现:在如图1中,小红和小明都发现:∠AEC=∠A+∠C;
小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A( )
∵EQ∥AB,AB∥CD.
∴EQ∥CD( )
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:两人的证明过程中,完全正确的是 .
(二)尝试:
(1)在如图2中,若∠A=110°,∠C=130°,则∠E的度数为 ;
(2)在如图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(三)探索:
装置如图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(四)猜想:
(1)如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(2)如图6,你可以得到什么结论?(直接写出结论)
【答案】(一) ( 两直线平行,内错角相等)(平行于同一条直线的两直线平行),小明的证法;(二)120°,30°;(三)见解析;(四) (1)∠E+∠G=∠B+∠F+∠D;(2)见解析.
【解析】
(一)小红、小明的做法,都是做了平行线,利用平行线的性质;(二)的(1)、(四)都可仿照(一),通过添加平行线把分散的角集中起来.
(一)( 两直线平行,内错角相等),(平行于同一条直线的两直线平行);
完全正确的是:小明的证法;
(二)尝试:
(1)(1)过点E作EF∥AB,
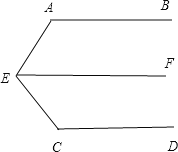
∵AB∥CD,
∴EF∥CD.∵EF∥AB,
∴∠A+∠AEF=180°,
∵∠A=110°,∴∠AEF=70°.
∵EF∥CD,
∴∠C+∠CEF=180°,
∵∠C=130°,∴∠CEF=50°.
∴∠AEC=∠AEF+∠CEF=70°+50°=120°.
(2)如图,

∵AB∥CD,
∴∠EOB=∠C=50°,
∵∠EOB=∠A+∠E,
∵∠E=∠EOB-∠A=50°-20°=30°.
答案:120°,30°.
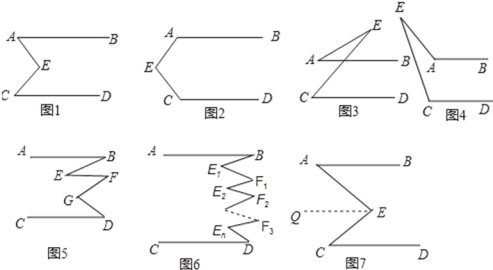
(三)∠E=∠EAB∠C.
理由:延长EA,交CD于点F.
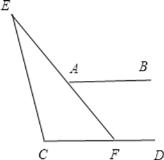
∵AB∥CD,
∴∠EFD=∠EAB.
∵∠EFD=∠C+∠E,
∴∠EAB=∠C+∠E,
∴∠E=∠EAB∠C.
(四)(1)可通过过点E、F、G分别做AB的平行线,得到结论:∠E+∠G=∠B+∠F+∠D.
(2)同上道理一样,可得到结论:∠E1+∠E2+…+∠En=∠F1+∠F2+…∠Fn+∠B+∠D.


科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
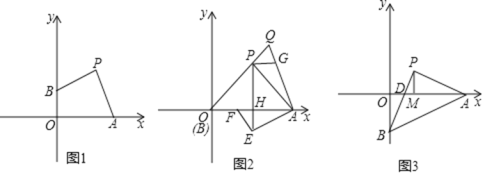
【题目】在平面直角坐标系中,点P在第一象限角平分线上,点A在x轴的正半轴运动,点B在y轴上,且![]() .
.
![]() 如图1,点B在y轴的正半轴上,
如图1,点B在y轴的正半轴上,![]() ,
,![]() ,则
,则![]() ______;
______;
![]() 如图2,点B与原点重合,
如图2,点B与原点重合,![]() ,点Q是OP延长线上一点,连接QA,过点P作
,点Q是OP延长线上一点,连接QA,过点P作![]() 轴,与QA相交于点G,过点P作x轴的垂线,垂足是点H,过点A作QA的垂线与PH相交于点E,过点E作
轴,与QA相交于点G,过点P作x轴的垂线,垂足是点H,过点A作QA的垂线与PH相交于点E,过点E作![]() ,与x轴相交于点F,若
,与x轴相交于点F,若![]() ,求点E的坐标;
,求点E的坐标;
![]() 如图3,点B在y轴的负半轴上,PB与x轴相交于点D,连接AB,AO平分
如图3,点B在y轴的负半轴上,PB与x轴相交于点D,连接AB,AO平分![]() ,过点P作
,过点P作![]() 轴于点M,求
轴于点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
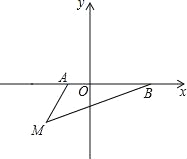
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:(1)求x,y的值;(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 . (只填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com