
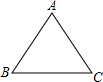
 点A运动.
点A运动.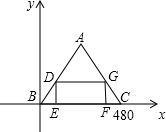
 =5
=5 t,
t, =5t
=5t ;
;
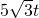 .然后由480-10t=
.然后由480-10t=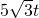
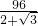 =96(2-
=96(2- )(毫米).所以当点D与点B的距离
)(毫米).所以当点D与点B的距离 )毫米时,矩形是正方形.
)毫米时,矩形是正方形.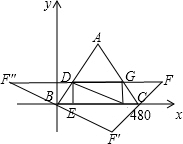
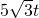 ,则面积是
,则面积是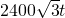 ;三角形ADC的底AD=480-10t,相应的高是240
;三角形ADC的底AD=480-10t,相应的高是240
 (480-10t).
(480-10t).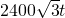 =120
=120 (480-10t),解得t=16
(480-10t),解得t=16 ),F′(400,-80
),F′(400,-80 )
) ).
).

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
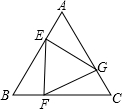 如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )A、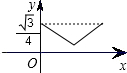 | B、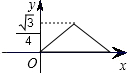 | C、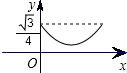 | D、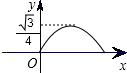 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 29、如图,已知正三角形的边长2a
29、如图,已知正三角形的边长2a查看答案和解析>>
科目:初中数学 来源: 题型:
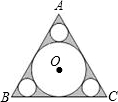 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 点A运动.
点A运动.查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com