Question

【题目】如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S四边形DGOF=2：7．其中正确结论的个数是（ ）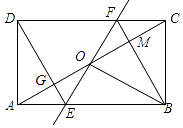
A.4个
B.3个
C.2个
D.1个

Answer 1

【答案】B
【解析】解：
①∵矩形ABCD中，O为AC中点，
∴OB=OC，
∵∠COB=60°，
∴△OBC是等边三角形，
∴OB=BC，
∵FO=FC，
∴FB垂直平分OC，
故①正确；
②∵△BOC为等边三角形，
∴OB=BC，
∵FO=FC，BF=BF，
∴△BCF≌△BOF，
∴∠BOF=∠BCF=90°，
∴BO⊥EF，
∵BF⊥OC，
∴∠CMB=∠EOB=90°，
∴BO≠BM，
∴△EOB与△CMB不全等；
故②错误；
③易知△ADE≌△CBF，∠1=∠2=∠3=30°，
∴∠ADE=∠1=30°，∠BEO=60°
∴∠CDE=60°，∠DFE=∠BEO=60°，
∴∠CDE=∠DFE，
∴DE=EF，
故③正确；
④易知△AOE≌△COF，
∴S△AOE=S△COF ，
∵S△COF=2S△CMF ，
∵∠FCO=30°，
∴FM= ，BM= CM，
∴ = ，
∴S△FOM：S△BOF=1：4，
易证△GEO≌△MFO，
∴S△GEO=S△MFO ，
易证明四边形DEBF是平行四边形，
∴S△DEF=S△EFB=2S△BOF，
设S△EGO=x，则S△AOE=2x，S△BOF=4x，
S四边形DGOF=S△DEF﹣S△EGO=S△EFB﹣S△EGO=8x﹣x，
∴S△AOE：S四边形DGOF=2x：（8x﹣x）=2：7，
故④正确；
所以其中正确结论的个数为3个；
故选B．
①利用线段垂直平分线的性质的逆定理可得结论；
②在△EOB和△CMB中，对应直角边不相等，则两三角形不全等；
③可证明∠CDE=∠DFE；
④设S△EGO=x，则S△AOE=2x，S△BOF=4x，可通过面积转化进行解答．