
分析 (1)把(-2,5)代入解析式,求出m;
(2)解一元二次方程求出点A、点B的坐标;
(3)设点C的坐标为(n,n2-2n-3),根据三角形的面积公式求出n的值,求出点C的坐标.
解答 解:(1)∵二次函数y=x2-(m-1)x-m的图象过点(-2,5),
∴(-2)2-(m-1)×(-2)-m=5,
解得,m=3;
(2)当m=3时,函数解析式为:y=x2-2x-3,
y=0时,x2-2x-3=0,
解得,x1=-1,x2=3,
∴点A的坐标为(-1,0)、点B的坐标为(3,0);
(3)设点C的坐标为(n,n2-2n-3),
∵点A的坐标为(-1,0)、点B的坐标为(3,0),
∴AB=4,
由题意得,$\frac{1}{2}$×4×|n2-2n-3|=8,
∴|n2-2n-3|=4,
当n2-2n-3=4时,n=1±2$\sqrt{2}$,
当n2-2n-3=-4时,n=1,
∴点C的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,4).
点评 本题考查的是抛物线与x轴的交点问题,掌握二次函数与一元二次方程的关系、灵活运用分情况讨论思想是解题的关键.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
 如图,点A,B是数轴上的两个点,点A表示的数为-4,点B在点A右侧,距离A点10个单位长度,动点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,点A,B是数轴上的两个点,点A表示的数为-4,点B在点A右侧,距离A点10个单位长度,动点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
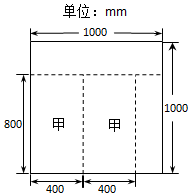 某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)
某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)| 方案一 | 方案二 | 方案三 | |
| 甲种型号瓷砖块数 | 1 | 2 | b |
| 乙种型号瓷砖块数 | a | 0 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
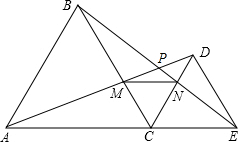 如图,点C为线段AE上任意一点,在AE同侧分别作等边三角形△ABC和等边三角形△CDE,连接AD,BE分别交BC,CD于点M,N,连接MN,则下列结论:
如图,点C为线段AE上任意一点,在AE同侧分别作等边三角形△ABC和等边三角形△CDE,连接AD,BE分别交BC,CD于点M,N,连接MN,则下列结论:| A. | ①②③④⑤ | B. | ①③④⑤ | C. | ①②④⑤ | D. | ①②③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
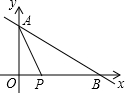 如图,已知一次函数y=-$\frac{1}{2}$x+4与两坐标轴分別交于A、B两点,动点P从原点0出发,以每秒2个单位的速度沿x轴正方向运动,连接AP,设运动时间为ts.
如图,已知一次函数y=-$\frac{1}{2}$x+4与两坐标轴分別交于A、B两点,动点P从原点0出发,以每秒2个单位的速度沿x轴正方向运动,连接AP,设运动时间为ts.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com