
【题目】下列条件中,不能判定四边形ABCD是平行四边形的是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】C
【解析】
根据平行四边形的判定条件,即可判断出正确答案.
A、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
故A可以判断四边形ABCD是平行四边形;
B、∵AB∥CD,∴∠B+∠C=180°,
∵∠B=∠D,
∴∠D+∠C=180°,
∴AC∥BD,
∴四边形ABCD是平行四边形,
故B可以判断四边形ABCD是平行四边形;
C、∵AB∥CD,AD=BC,
∴四边形ABCD可能是平行四边形,有可能是等腰梯形.
故C不可以判断四边形ABCD是平行四边形
D、∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
故D可以判断四边形ABCD是平行四边形;
故选:C.


科目:初中数学 来源: 题型:
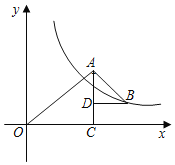
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,OC边在x轴上点A、D、C共线,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC和△BAD的面积之差为_____(用含k的代数式表示).
在第一象限的图象经过点B,则△OAC和△BAD的面积之差为_____(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题背景]![]() 三边的长分别为
三边的长分别为![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解这道题时,先建立一个正方形网格(每个小正方形的边长为![]() ),再在网格中作出格点
),再在网格中作出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),如图1所示,这样不需要作
三个顶点都在小正方形的顶点处),如图1所示,这样不需要作![]() 的高,借用网格就能计算出
的高,借用网格就能计算出![]() 的面积为_ ;
的面积为_ ;

[思维拓展]我们把上述求![]() 面积的方法叫做构图法,若
面积的方法叫做构图法,若![]() 三边的长分别为
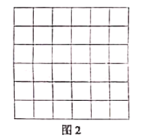
三边的长分别为![]() ,请利用图2的正方形网格(每个小正方形的边长为
,请利用图2的正方形网格(每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积:
,并求出它的面积:
[探索创新]若![]() 三边的长分别为
三边的长分别为![]() (其中
(其中![]() 且
且![]() ),请利用构图法求出这个三角形的面积(画出图形并计算面积).
),请利用构图法求出这个三角形的面积(画出图形并计算面积).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,![]() ,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
(1)求证:四边形CDBE为矩形;
(2)若AC=2,![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
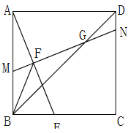
【题目】已知,正方形ABCD中,点E为BC边上任意一点(点E不与B,C重合),点F在线段AE上,过点F的直线![]() ,分别交AB、CD于点M、N.
,分别交AB、CD于点M、N.
(1)如图,求证:![]() ;
;

(2)如图,当点F为AE中点时,连接正方形的对角线BD,MN与BD交于点G,连接BF,求证:![]() ;
;
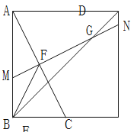
(3)如图,在(2)的条件下,若![]() ,
,![]() ,求BM的长度.
,求BM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
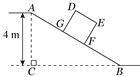
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com