
【题目】如图,已知点M、N分别为ABCD的边CD、AB的中点,连接AM、CN. 
(1)证明:AM=CN;
(2)过点B作BH⊥AM于点H,交CN于点E,连接CH,判断线段CB、CH的数量关系,并说明理由. 
【答案】
(1)AM∥NC,
理由:∵点M、N分别为ABCD的边CD、AB的中点,
∴AB=CD,MC=AN,AB∥CD,
∴AN∥MC,AN=MC,
∴四边形ANCM是平行四边形,
∴AM∥NC
(2)解:BC=HC,
理由:∵AM∥NC,AN=BN,
∴BE=HE,
∵BH⊥AM,
∴EB⊥NE,
∴NC垂直平分HB,
∴HC=BC
【解析】(1)利用平行四边形的性质得出AN∥MC,AN=CM,进而利用平行四边形的判定得出答案;(2)利用三角形中位线定理的推论得出HE=EB,以及利用平行线的性质得出NC⊥HB,再利用线段垂直平分线的性质得出答案.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数的图象与反比例函数的图象都经过点P(2,3),点D是正比例函数图象上的一点,过点D作y轴的垂线,垂足分别Q,DQ交反比例函数的图象于点A,过点A作x轴的垂线,垂足为B,AB交正比例函数的图于点E.
(1)求正比例函数解析式、反比例函数解析式.
(2)当点D的纵坐标为9时,求:点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一游戏棋盘和一个质地均匀的正四面体骰子(各面依次标有1,2,3,4四个数字).游戏规则是游戏者每掷一次骰子,棋子按着地一面所示的数字前进相应的格数.例如:若棋子位于A处,游戏者所掷骰子着地一面所示数字为3,则棋子由A处前进3个方格到达B处.请用画树形图法(或列表法)求掷骰子两次后,棋子恰好由A处前进6个方格到达C处的概率. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE∥BC,∠ADE=48°,则下列结论中不正确的是( ) 
A.∠B=48°
B.∠AED=66°
C.∠A=84°
D.∠B+∠C=96°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E . 若∠A=60°,BC=6,则图中阴影部分的面积为
A.![]() π
π
B.![]() π
π
C.![]() π
π
D.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 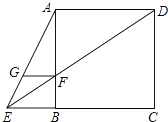
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com