
)如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=![]() x+3的图象与y轴的交点,点B在二次函数
x+3的图象与y轴的交点,点B在二次函数![]() 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
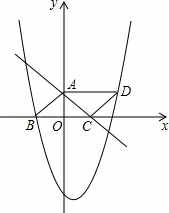
考点:二次函数综合题.
分析:(1)根据一次函数解析式求出点A.点C坐标,再由△ABC是等腰三角形可求出点B坐标,根据平行四边形的性性质求出点D坐标,利用待定系数法可求出b、c的值,继而得出二次函数表达式.
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,再由△APQ∽△CAO,利用对应边成比例可求出t的值,继而确定点P的位置;
②只需使△APQ的面积最大,就能满足四边形PDCQ的面积最小,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO,利用对应边成比例得出h的表达式,继而表示出△APQ的面积表达式,利用配方法求出最大值,即可得出四边形PDCQ的最小值,也可确定点P的位置.
解答:解:(1)由y=﹣![]() x+3,
x+3,
令x=0,得y=3,所以点A(0,3);
令y=0,得x=4,所以点C(4,0),
∵△ABC是以BC为底边的等腰三角形,
∴B点坐标为(﹣4,0),
又∵四边形ABCD是平行四边形,
∴D点坐标为(8,3),
将点B(﹣4,0)、点D(8,3)代入二次函数y=![]() x2+bx+c,可得
x2+bx+c,可得![]() ,
,
解得: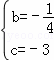 ,
,
故该二次函数解析式为:y=![]() x2﹣
x2﹣![]() x﹣3.
x﹣3.
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,
∵PQ⊥AC,
∴△APQ∽△CAO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:t=![]() .
.
即当点P运动到距离A点![]() 个单位长度处,有PQ⊥AC.
个单位长度处,有PQ⊥AC.
②∵S四边形PDCQ+S△APQ=S△ACD,且S△ACD=![]() ×8×3=12,
×8×3=12,
∴当△APQ的面积最大时,四边形PDCQ的面积最小,
当动点P运动t秒时,AP=t,CQ=t,AQ=5﹣t,
设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO可得:![]() =
=![]() ,
,
解得:h=![]() (5﹣t),
(5﹣t),
∴S△APQ=![]() t×
t×![]() (5﹣t)=
(5﹣t)=![]() (﹣t2+5t)=﹣
(﹣t2+5t)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,S△APQ达到最大值
时,S△APQ达到最大值![]() ,此时S四边形PDCQ=12﹣
,此时S四边形PDCQ=12﹣![]() =
=![]() ,
,
故当点P运动到距离点A![]() 个单位处时,四边形PDCQ面积最小,最小值为
个单位处时,四边形PDCQ面积最小,最小值为![]() .
.
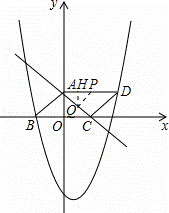
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、平行四边形的性质、相似三角形的判定与性质,解答本题的关键是找到满足题意时的相似三角形,利用对应边成比例的知识得出有关线段的长度或表达式,难度较大.


科目:初中数学 来源: 题型:
 如图,三角形ABC三个顶点的坐标分别为A(2,3),B(-2,0),C(5,O),将三角形ABC沿x轴负方向平移2个单位,再沿y轴负方向平移1个单位,得到三角形A1B1C1.
如图,三角形ABC三个顶点的坐标分别为A(2,3),B(-2,0),C(5,O),将三角形ABC沿x轴负方向平移2个单位,再沿y轴负方向平移1个单位,得到三角形A1B1C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com