解:(1)原式=9+1-125÷25
=9+1-5
=5;
(2)原式=(

×1.5)
2008×(

)×(-1)
2009
=1×

×(-1)
=-

;
(3)原式=64a
6-9a
6+64a
6
=119a
6;
(4)原式=-3x
2+3xy+2xy-2x
2
=-5x
2+5xy;
(5)原式=m
2-(

n
2)
=m
2-

n
2;
(6)原式=4x
2+9y
2-12xy-(3xy-y
2+9x
2-3xy)
=4x
2+9y
2-12xy+y
2-9x
2
=-5x
2+10y
2-12xy;
(7)原式=4m
2-2mn+2mp+2mn-n
2+np-2mp+np-p
2
=4m
2-n
2-p
2+2np;
(8)原式=x
3m•x
2n=(x
m)
3•(x
n)
2,
∵x
m=3,x
n=2,
∴原式=3
3×2
2=27×4=108.
分析:(1)先分别根据负整数指数幂、0指数幂及有理数的乘方法则分别计算出各数,再根据有理数混合运算的法则进行计算;
(2)根据幂的乘方与积的乘方法则进行计算;
(3)先根据幂的乘方与积的乘方计算出各数,再合并同类项即可;
(4)先去括号,再合并同类项;
(5)直接根据平方差公式进行计算即可;
(6)分别根据完全平方公式及平方差公式计算出各数,再合并同类项;
(7)先根据整式的乘法计算出各数,再合并同类项即可;
(8)先根据幂的乘方与积的乘方法则把原式化为(x
m•x
n)
2的形式,再把x
m=3,x
n=2代入进行计算.
点评:本题考查的是整式的混合运算、有理数的混合运算及幂的乘方与积的乘方法则,在解答此类题目时要注意各种运算律的灵活运用.

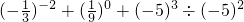
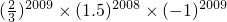
 n)
n)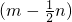
 ×1.5)2008×(
×1.5)2008×( )×(-1)2009
)×(-1)2009 ×(-1)
×(-1) ;
; n2)
n2) n2;
n2;

 阅读快车系列答案
阅读快车系列答案