
【题目】在数轴上有三个点A、B、C(如图).请回答:
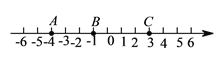
(1)写出数轴上与点B相距5个单位的点M所表示的数为 ;
(2)在数轴上表示:将点C向左移动6个单位到达点D,点A的相反数为点E,并用“<”号把B、D、E三点所表示的数连接起来.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( ) 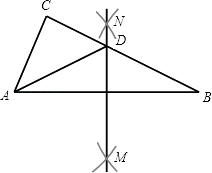
A.7
B.14
C.17
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮? 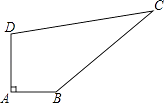
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如下表:
每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
人数 | 2 | 5 | 8 | 9 | 6 |
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.4,3
B.4,3.5
C.3.5,3.5
D.3.5,4
查看答案和解析>>
科目:初中数学 来源: 题型:
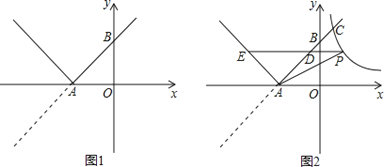
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
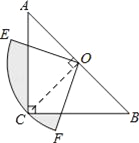
【题目】如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
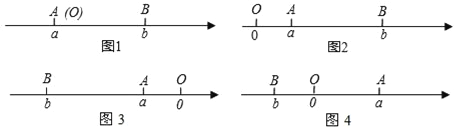
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com