
【题目】△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一角顶点B在y轴上.
(1)如图①若AD⊥x轴,垂足为点D.点C坐标是(﹣1,0),点B的坐标是(0,2),求A点的坐标.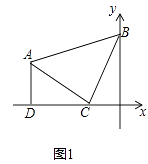
(2)如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,求证:BD=2AE.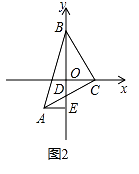
(3)如图③,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论:① ![]() 为定值;②
为定值;② ![]() 为定值,只有一个结论成立,请你判断正确的结论并求出定值.
为定值,只有一个结论成立,请你判断正确的结论并求出定值.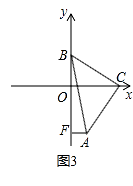
【答案】
(1)
解:∵∠ACB=90°,
∴∠ACD+∠BCO=90°,
∵AD⊥CD,
∴∠ACD+∠CAD=90°,
∴∠BCO=∠CAD,
在△ACD和△CBO中, 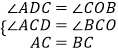 ,
,
∴△ACD≌△CBO,
∴AD=CO=1,DC=OB=2,
∴OD=OC+CD=3,
∴A(﹣3,1)
(2)
解:如图,
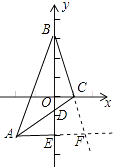
延长AE、BC交于点F,
∵y轴平分∠ABC,AE⊥y轴,
∴AE=EF,
∴AF=2AE,
∵AE⊥x轴,
∴∠EAD+∠ADE=90°,
∵∠ADE=∠BDC,
∴∠EAD+∠BDC=90°,
∵∠ABC=90°,
∴∠BDC+∠CBD=90°,
∴∠DAE=∠CBD,
在△BCD和△ACF中, 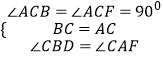 ,
,
∴△BCD≌△ACF,
∴BD=AF,
∵AF=2AE,
∴BD=2AE
(3)
解:① ![]() 为定值,理由:
为定值,理由:
如图3,
作AE⊥OC于E,
∵∠ACB=90°,
∴∠OCB+∠OCA=90°,
∵∠OBC+∠OCB=90°,
∴∠OCA=∠OBC,
在△OBC和△ECA中  .
.
∴△OBC≌△ECA,
∴OB=CE,
∵AF=OE
∴① ![]() =
= ![]() =
= ![]() =1是定值,
=1是定值,
② ![]() =
= ![]() =
= ![]() =
= ![]() +
+ ![]() =
= ![]() +1,而2AF与AB的关系不知,
+1,而2AF与AB的关系不知,
∴②不是定值.
即:① ![]() 为定值
为定值
【解析】(1)先判断出,∠BCO=∠CAD,从而得出△ACD≌△CBO,求出AD=CO=1,DC=OB=2即可;(2)先利用等腰三角形的判定得出AF=2AE,同(1)的方法判断出△BCD≌△ACF,得出BD=AF即可;(3)作AE⊥OC,同(1)方法判断出△OBC≌△ECA得出OB=CE,最后结合图形求出①个结论是定值.
【考点精析】通过灵活运用等腰三角形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜:
(1)请你写出C、E所表示的意义.
(2)若一只兔子从A顺着方格线向上或向右移动到达B,试问有几条路径可供选择,其中走哪条路径吃到的胡萝卜最多?走哪条路径吃到的小白菜最多?请你通过计算的方式说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上的点P(2,﹣1)向上平移2个单位,再向左平移1个单位后,点P的坐标变为( )
A.(2,1)
B.(1,1)
C.(﹣2,1)
D.(4,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com