

分析 (1)根据列出与时间的关系可以确定t的范围,根据t=1时,△APE面积为1,即可求出AE.
(2)只要证明∠MAD=∠MFD=30°即可解决问题.
(3))①若∠PQH为直角三角形,△APQ∽△DQH,得$\frac{AP}{DQ}$=$\frac{AQ}{DH}$,求出DH=$\frac{4-t}{2}$,再由DH∥AP,得$\frac{DH}{AP}$=$\frac{DF}{AF}$列出方程即可解决.
②若∠PHQ=90°,如图4中,作PM⊥CD于M,类似①利用相似三角形性质列出方程即可解决问题.
解答 解:(1)∵AB=7,7÷2=3.5,
∴0≤t≤3.5,
由图象可知y=t,
∴t=1时,y=1,
∴$\frac{1}{2}$•AE•2=1,
∴AE=1,
故答案分别为0≤t≤3.5,1.
(2)如图3中,∵四边形AMHP是菱形,
∴AM=MH=2DM,AM∥PF,
∵∠ADM=90°,
∴∠MAD=30°,
∴∠PFA=∠MFA=∠MAD=30°,
∴MA=MF,∵MD⊥AF,
∴AD=DF=4,
∴a=4.AP=2DM=$\frac{8\sqrt{3}}{3}$,
∴t=$\frac{4\sqrt{3}}{3}$.
(3)①若∠PQH为直角三角形,
∵∠PQA+∠HQD=90°,∠HQD+∠QHD=90°,
∴∠AQP=∠QHD,∵∠PAQ=∠HDQ=90°.
∴△APQ∽△DQH,
∴$\frac{AP}{DQ}$=$\frac{AQ}{DH}$,
∴$\frac{2t}{4-t}$=$\frac{t}{DH}$,
∴DH=$\frac{4-t}{2}$,
∵DH∥AP,
∴$\frac{DH}{AP}$=$\frac{DF}{AF}$,
∴$\frac{\frac{4-t}{2}}{2t}$=$\frac{\frac{4}{3}}{4+\frac{4}{3}}$,
∴t=2.
②若∠PHQ=90°,如图4中,作PM⊥CD于M,同理可证△PMH∽△HDQ,
∴$\frac{PM}{HD}$=$\frac{MH}{DQ}$,
∴$\frac{4}{HD}$=$\frac{2t-HD}{4-t}$,
∵DH∥AP,
∴$\frac{DH}{AP}$=$\frac{DF}{AF}$,
∴$\frac{DH}{2t}$=$\frac{\frac{4}{3}}{4+\frac{4}{3}}$,
∴DH=$\frac{1}{2}$t,
∴$\frac{4}{\frac{1}{2}t}$=$\frac{2t-\frac{1}{2}t}{4-t}$,
∴3t2+16t-64=0,
∴t=$\frac{8}{3}$或(-8舍弃),
∴t=2或$\frac{8}{3}$时,△PQH能构成直角三角形.
点评 本题考查四边形综合题、相似三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质,列出方程解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )| A. | 14 | B. | 22斛 | C. | 36斛 | D. | 66斛 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.55×107 | B. | 0.855×109 | C. | 8.55×108 | D. | 85.5×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
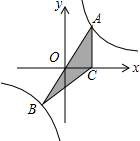 如图,已知经过原点的直线AB与反比例函数y=$\frac{k}{x}$(k≠0)图象分别相交于点A和点B,过点A作AC⊥x轴于点C,若△ABC的面积为4,则k的值为( )
如图,已知经过原点的直线AB与反比例函数y=$\frac{k}{x}$(k≠0)图象分别相交于点A和点B,过点A作AC⊥x轴于点C,若△ABC的面积为4,则k的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥2 | B. | m>2 | C. | m≤2 | D. | m<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
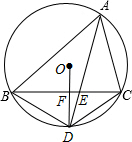 如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )
如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com