
已a是方程x2﹣2018x+1=0的一个根a,则a2﹣2017a+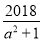 的值为_____.
的值为_____.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:解答题
已知关于 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
⑴求 的取值范围;
的取值范围;
⑵若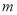 为整数且
为整数且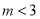 ,
,  是方程的一个根,求代数式
是方程的一个根,求代数式 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年七年级上学期期末数学试卷 题型:单选题
下列各式 ,
,  ,
, 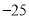 ,
, 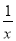 ,
,  ,
, 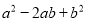 中单项式的个数有( )
中单项式的个数有( )
A.  个 B.
个 B.  个 C.
个 C.  个 D.
个 D. 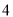 个
个
查看答案和解析>>
科目:初中数学 来源:广西柳州市2018届九年级上学期期末考试数学试卷 题型:填空题
方程x2-3x+2=0 的二次项系数是________.
1 【解析】一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项, 所以方程x2-3x+2=0 的二次项系数是1, 故答案为:1.查看答案和解析>>
科目:初中数学 来源:广西柳州市2018届九年级上学期期末考试数学试卷 题型:单选题
关于x的一元二次方程(a2﹣1)x2+x﹣2=0是一元二次方程,则a满足( )
A. a≠1 B. a≠﹣1 C. a≠±1 D. 为任意实数
C 【解析】试题分析:一元二次方程是指只含有一个未知数,且未知数最高次数为2次的整式方程.根据定义可得:,解得:.查看答案和解析>>
科目:初中数学 来源:重庆市2018届九年级(上)入学数学试卷(9月份) 题型:单选题
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<﹣1;④b2+8a>4ac.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】①4a-2b+c<0;当x=-2时,y=ax2+bx+c,y=4a-2b+c,由-2<x1<-1,可得y<0,故①正确; ②2a-b<0;已知x=- >-1,且a<0,所以2a-b<0,故②正确; ③已知抛物线经过(-1,2),即a-b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),联立(1)(2),得:a+c<1;所以③正确 ④由于抛物线的...查看答案和解析>>
科目:初中数学 来源:重庆市2018届九年级(上)入学数学试卷(9月份) 题型:单选题
融侨半岛某文具店购入一批笔袋进行销售,进价为每个20元,当售价为每个50元时,每星期可以卖出100个,现需降价处理:售价每降价3元,每星期可以多卖出15个,店里每星期笔袋的利润要达到3125元.若设店主把每个笔袋售价降低x元,则可列方程为( )
A. (30+x)(100-15x)=3125 B. (30﹣x)(100+15x)=3125
C. (30+x)(100-5x)=3125 D. (30﹣x)(100+5x)=3125
D 【解析】试题解析:若设店主把每个笔袋售价降低x元,根据总利润达到3125元列出方程:(30﹣x)(100+5x)=3125,故选D.查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试八年级数学试卷 题型:填空题
若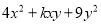 是一个完全平方式,则k的值为___________.
是一个完全平方式,则k的值为___________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海口市八年级数学科期末检测模拟题(普通班卷) 题型:解答题
计算
(1)2x2(3x-y);
(2)(3a+1)(a-2);
(3)(3x-y)2 ;
(4)102×98(用简便方法计算).
(1)6x3-2x2y(2)3a2-5a-2(3)9x2-6xy+y2(4)9996 【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可; (2)原式利用多项式乘以多项式展开,合并后即可得到结果; (3)原式利用完全平方公式展开即可得到结果; (4)原式变形后,利用平方差公式化简即可得到结果. 试题解析:(1)原式=6x 3 -2x 2 y; (2)原...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com