某公司需在一个月(31天)内完成新建办公楼的装修工程.若甲、乙两个工程队合作8天,
则其余的工作乙要10天才能完成,这样共需装修费用为41200元;若甲先做10天,然后乙做15天才能完成这工程,这样共需装修费用为41000元.
(1)只要求在规定的时间内完成工程,若只请一个工程队,请问可以请哪个工程队?
(2)在规定的时间内完成工程,按方案A:单独请一个工程队单独完成此项工程;方案B:请甲、乙两个工程队合作完成此项工程.试问哪一种方案花钱少?
分析:(1)设甲工程队单独做需x天完成,乙工程队单独做需y天完成.根据等量关系:①甲、乙两个工程队合作8天,则其余的工作乙要10天才能完成,②甲先做10天,然后乙做15天才能完成这工程,列方程组求解,求得的值和规定时间31天比较得出结论;
(2)设甲工程队每天的装修费用为a元,乙工程队每天的装修费用为b元.根据等量关系:①甲、乙两个工程队合作8天,则其余的工作乙要10天才能完成,这样共需装修费用为41200元,得8a+18b=41200;②甲先做10天,然后乙做15天才能完成这工程,这样共需装修费用为41000元,得10a+15b=41000,列方程组求解.再进一步根据独作、合作的时间计算所需费用,最后比较得出结论.
解答:解:(1)设甲工程队单独做需x天完成,乙工程队单独做需y天完成,
由题可得
,
解得
.
∵x=20<31,y=30<31
∴甲乙两个工程队都可以请;
(2)设甲工程队每天的装修费用为a元,乙工程队每天的装修费用为b元,
由题可得
| | 8(a+b)+10b=41200 | | 10a+15b=41000 |
| |
,
解得
.
单独请甲工程队需20×2000=40000(元).
单独请乙工程队需30×1400=42000(元).
甲乙合作需
1÷(+)×(2000+1400)=40800(元).
∵40000<40800<42000,
∴单独请甲工程队完成所需的费用最少.
点评:此题首先要把工作量看作单位1.根据公式:工作量=工作时间×工作效率,列方程组求得两队独做分别需要的时间;根据费用=时间×每天的费用,列方程组分别求得两队每天的费用.



 名校课堂系列答案
名校课堂系列答案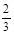 .
. .
.