
【题目】已知二次函数y=﹣x2+x+m.
(1)如图,二次函数的图象过点A(3,0),与y轴交于点B,求直线AB和二次函数图象的解析式;
(2)在线段AB上有一动点P(不与A,B两点重合),过点P作x轴的垂线,交抛物线于点D,是否存在一点P使线段PD的长有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
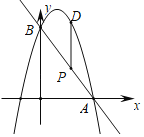
【答案】(1)y=﹣2x+6,y=﹣x2+x+6;(2)存在P(![]() ,3)
,3)
【解析】
(1)把点A(3,0)代入y=﹣x2+x+m得到﹣9+3+m=0,求出m得到抛物线解析式和B点坐标,然后根据待定系数法求直线AB的解析式;
(2)设P(x,﹣2x+6),则D(x,﹣x2+x+6),那么PD=(﹣x2+x+6)﹣(﹣2x+6)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() ,根据二次函数的性质即可得到结论.
,根据二次函数的性质即可得到结论.
解:(1)∵点A(3,0)在抛物线y=﹣x2+x+m上,
∴﹣9+3+m=0,
∴m=6,
∴抛物线解析式为y=﹣x2+x+6,且B(0,6),
设直线AB的解析式为y=kx+b,
将A(3,0),B(0,6)代入y=kx+b中,得![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=﹣2x+6;
(3)设P(x,﹣2x+6),则D(x,﹣x2+x+6),
∴PD=(﹣x2+x+6)﹣(﹣2x+6)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() ,
,
∵a=﹣1<0,
∴当x=![]() 时,线段PD的长有最大值为
时,线段PD的长有最大值为![]() ,
,
当x=![]() 时,y=﹣2x+6=3,
时,y=﹣2x+6=3,
∴P(![]() ,3).
,3).


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个小组各10名同学进行英语口语会话练习,各练5次,他们每个同学合格的次数分别如下:
甲组:4,1,2,2,1,3,3,1,2,1;
乙组:4,3,0,2,1,3,3,0,1,3.
根据上述信息画折线统计图,并根据统计图指出哪个小组的口语会话的合格次数比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并解决问题:一般地,如果把一个图形绕着一个定点旋转一定角度![]() (
(![]() 小于
小于![]() )后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.
)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.![]() 叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
(1)请写出一个旋转对称图形,这个图形有一个旋转角是![]() .这个图形可以是______;
.这个图形可以是______;
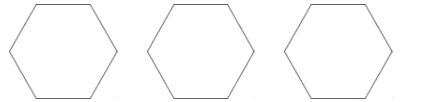
(2)为了美化环境,某中学需要在一块正六边形空地上分别种植六种不同的花草,现将这块空地按下列要求分成六块:①分割后的整个图形必须既是轴对称图形又是旋转对称图形;②六块图形的面积相同.请你按上述两个要求,分别在图中的三个正六边形中画出三种不同的分割方法(只要求画图正确,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
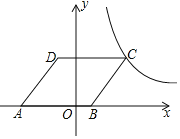
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com