
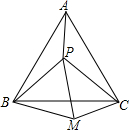
 如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM.
如图,P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作等边三角形BPM,连接CM. :
: ,试判断△PMC的形状,并说明理由.
,试判断△PMC的形状,并说明理由. :
: ,
, :
: .
. k,PC=
k,PC= k,
k, :
: .我们发现这三边正好符合勾股定理的要求.因此三角形PMC是直角三角形.
.我们发现这三边正好符合勾股定理的要求.因此三角形PMC是直角三角形.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,△ABC是等边三角形纸片,沿EF翻折,使点A落在BC边上的D点,设∠AEF=a,AE=x,AF=y.
如图,△ABC是等边三角形纸片,沿EF翻折,使点A落在BC边上的D点,设∠AEF=a,AE=x,AF=y.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•历下区一模)如图,△ABC是等边三角形,△DEF是边长为7的等边三角形,点B与点E重合,点A、B、(E)、F在同一条直线上,将△ABC沿E→F方向平移至点A与点F重合时停止,设点B、E之间的距离为x,△ABC与△DEF重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是( )
(2012•历下区一模)如图,△ABC是等边三角形,△DEF是边长为7的等边三角形,点B与点E重合,点A、B、(E)、F在同一条直线上,将△ABC沿E→F方向平移至点A与点F重合时停止,设点B、E之间的距离为x,△ABC与△DEF重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是( )查看答案和解析>>
科目:初中数学 来源: 题型:
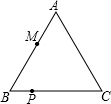 (2013•海淀区一模)如图,△ABC是等边三角形,AB=6厘米,点P从点B出发,沿BC以每秒1厘米的速度运动到点C停止;同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动,则另一个点也停止运动.设点P的运动时间为t秒,P、M两点之间的距离为y厘米,则表示y与t的函数关系的图象大致是( )
(2013•海淀区一模)如图,△ABC是等边三角形,AB=6厘米,点P从点B出发,沿BC以每秒1厘米的速度运动到点C停止;同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动,则另一个点也停止运动.设点P的运动时间为t秒,P、M两点之间的距离为y厘米,则表示y与t的函数关系的图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE.
如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com