
【题目】如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.
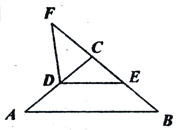
(l)若AB=1O,求FD的长;
(2)若AC=BC.求证:△CDE∽△DFE .
【答案】(1) FD=5; (2)证明见解析.
【解析】试题分析:(1)利用三角形中位线的性质得出DE∥AB,进而得出∠DEC =∠B,即可得出FD=DE,即可得出答案;
(2)利用等腰三角形的性质和平行线的性质得出∠B=∠A=∠CED=∠CDE,即可得出∠CDE=∠F,即可得出△CDE∽△DFE.
试题解析:解:(1)∵D、E分别是AC、BC的中点,∴.DE//AB, DE=![]() AB=5.
AB=5.
又∵DE//AB,∴∠DEC= ∠B.而∠ F= ∠ B,∴∠DEC =∠B,∴FD=DE=5;
(2)∵AC=BC,∴∠A=∠B.又∠CDE=∠A,∠CED= ∠B,∴∠CDE=∠B.
而∠B=∠F,∴∠CDE=∠F,∠CED=∠DEF,∴△CDE∽△DFE .


科目:初中数学 来源: 题型:
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
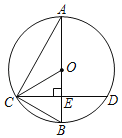
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 边的中点,沿
边的中点,沿![]() 对折矩形
对折矩形![]() ,使
,使![]() 点落在
点落在![]() 处,折痕为
处,折痕为![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() 点.
点.
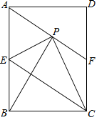
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若矩形![]() 的边
的边![]() =
=![]() ,
,![]() =
=![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
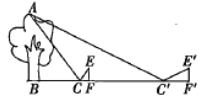
【题目】小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离.于是他利用镜子进行两次测量.如图,第一次他把镜子放在点C处,人在点F处正好在镜中看到树尖A;第二次他把镜子放在点![]() 处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得
处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得![]() m,
m,![]() m,
m,![]() m.求这棵古松树的高度.
m.求这棵古松树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】例:利用函数图象求方程x2﹣2x﹣2=0的实数根(结果保留小数点后一位).
解:画出函数y=x2﹣2x﹣2的图象,它与x轴的公共点的横坐标大约是﹣0.7,2.7.所以方程x2﹣2x﹣2=0的实数根为x1≈﹣0.7,x2≈2.7.我们还可以通过不断缩小根所在的范围估计一元二次方程的根.……这种求根的近似值的方法也适用于更高次的一元方程.
根据你对上面教材内容的阅读与理解,解决下列问题:
(1)利用函数图象确定不等式x2﹣4x+3<0的解集是 ;利用函数图象确定方程x2﹣4x+3=![]() 的解是 .
的解是 .
(2)为讨论关于x的方程|x2﹣4x+3|=m解的情况,我们可利用函数y=|x2﹣4x+3|的图象进行研究.
①请在网格内画出函数y=|x2﹣4x+3|的图象;
②若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解,则m的取值范围为 ;
③若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解x1,x2,x3,x4(x1<x2<x3<x4),满足x4﹣x3=x3﹣x2=x2﹣x1,求m的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是______.
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AD是⊙O的直径,AD=12,点BC在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°,则以下判断中不正确的是( )
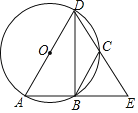
A.∠ADE=∠EB.劣弧AB的长为![]() π
π
C.点C为弧BD的中点D.BD平分∠ADE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com