
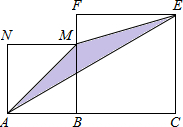
 AME的面积记为Sn.当n≥2时,Sn-Sn-1=
AME的面积记为Sn.当n≥2时,Sn-Sn-1=| 2n-1 |
| 2 |
| 2n-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 解:方法一:连接BE.
解:方法一:连接BE.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2n-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2n-1 |
| 2 |
| 2n-1 |
| 2 |


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
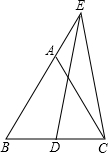 (2012•天门)如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( )
(2012•天门)如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•天门)如图,海中有一小岛B,它的周围15海里内有暗礁.有一货轮以30海里/时的速度向正北航行,当它航行到A处时,发现B岛在它的北偏东30°方向,当货轮继续向北航行半小时后到达C处,发现B岛在它的东北方向.问货轮继续向北航行有无触礁的危险?(参考数据:
(2012•天门)如图,海中有一小岛B,它的周围15海里内有暗礁.有一货轮以30海里/时的速度向正北航行,当它航行到A处时,发现B岛在它的北偏东30°方向,当货轮继续向北航行半小时后到达C处,发现B岛在它的东北方向.问货轮继续向北航行有无触礁的危险?(参考数据:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
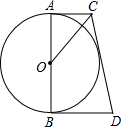 (2012•天门)如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD.
(2012•天门)如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com