
【题目】如图,在△ABC 中,∠A=∠B=30°,E,F 在 AB 上,∠ECF=60°.
(1)画出△BCF 绕点 C 顺时针旋转 120°后的△ACK;
(2)在(1)中,若 AE2+ EF2= BF2,求证 BF=![]() CF.
CF.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)旋转后CB与CA重合,作∠KCA=∠FCB,截取KC=FC即可;(2)连结KE,作KH⊥AC于H,先得到∠ACE+∠BCF=60°,再根据旋转的性质得BF=AK,∠KCA=∠FCB,CK=CF,∠KAC=∠B=30°,则∠KCE=∠FCE,可根据“SAS”判断△CKE≌△CFE,所以KE=EF,由于AE2+EF2=BF2,则AE2+KE2=AK2,根据勾股定理的逆定理得∠AEK=90°,且∠KEC=∠FEC=45°,可计算∠BCF=45°,设KH=a,在Rt△KHC中可得KC=![]() a;在Rt△KHA中得AK=2a,所以AK:KC=2a:
a;在Rt△KHA中得AK=2a,所以AK:KC=2a:![]() a=
a=![]() ,则BF:CF=
,则BF:CF=![]() ,由此即可得结论.
,由此即可得结论.
(1)如图,
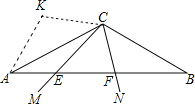
(2)证明:连结KE,作KH⊥AC于H,如图,
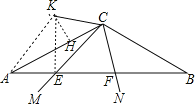
∵∠A=∠B=30°,∠MCN=60°,
∴∠ACB=120°,
∴∠ACE+∠BCF=60°,
∵△BCF绕点C顺时针旋转120゜后的△ACK,
∴BF=AK,∠KCA=∠FCB,CK=CF,∠KAC=∠B=30°,
∴∠KCE=∠KCA+∠ACE=∠FCB+∠ACE=60°,
∴∠KCE=∠FCE,
在△CKE和△CFE中,
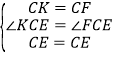 ,
,
∴△CKE≌△CFE,
∴KE=EF,∠KEC=∠FEC,
∵AE2+EF2=BF2,
∴AE2+KE2=AK2,
∴△AEK为直角三角形,
∴∠AEK=90°,
∴∠KEC=∠FEC=45°,
∴∠BCF=180°-45°-60°-30°=45°,
∴∠KCA=45°,
设KH=a,在Rt△KHC中,KC=![]() a;
a;
在Rt△KHA中,∠KAC =30°,
∴AK=2a,
∴AK:KC=2a:![]() a=
a=![]() ,
,
∴BF:CF=![]() ,
,
即BF=![]() CF.
CF.


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点![]() .
.
![]() 写出函数表达式;
写出函数表达式;
![]() 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限?![]() 随
随![]() 的增大怎样变化?
的增大怎样变化?
![]() 点
点![]() 、
、![]() 在这个函数的图象上吗?
在这个函数的图象上吗?
![]() 如果点
如果点![]() 在图象上,求
在图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM=AN,点B和点C分别为∠MAN两边上的点,AB=AC.按下列语句画出图形:(要求用无刻度直尺作图,)
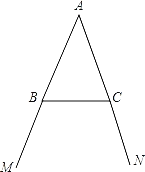
(1)AD⊥BC,垂足为D;
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店某几种型号的计算器每只进价 12 元、售价 20 元,多买优惠, 优惠方法是:凡是一次买 10 只以上的,每多买一只,所买的全部计算器每只就 降价 0.1 元,例如:某人买 18 只计算器,于是每只降价 0.1×(18-10)=0.8(元), 因此所买的 18 只计算器都按每只 19.2 元的价格购买,但是每只计算器的最低售 价为 16 元.
(1)求一次至少购买多少只计算器,才能以最低售价购买? (2)写出该文具店一次销售 x(x>10)只时,所获利润 y(元)与 x(只)之间的函数关系 式,并写出自变量 x 的取值范围;
(3)一天,甲顾客购买了 46 只,乙顾客购买了 50 只,店主发现卖 46 只赚的钱反 而比卖 50 只赚的钱多,请你说明发生这一现象的原因;当 10<x≤50 时,为了 获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等边三角形,点E在线段AB上,点D在直线BC上,且
是等边三角形,点E在线段AB上,点D在直线BC上,且![]() ,将
,将![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() 至
至![]() ,连接EF.
,连接EF.
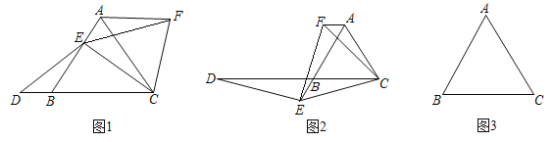
(1)证明:![]() ;
;
(2)如图2,如果点E在线段AB的延长线上,其他条件不变,请你写出线段AB、DB、AF之间的数量关系,并证明你的结论;
(3)如果点E在线段BA的延长线上,其他条件不变,请在图3的基础上将图形补充完整,并写出AB、DB、AF之间的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2018年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.
(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了![]() %,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
%,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交AC于点D,动点P在抛物线对称轴上,动点Q在抛物线上.
(1)求抛物线的解析式;
(2)当PO+PC的值最小时,求点P的坐标;
(3)是否存在以A,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com