
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.分析 (1)根据垂径定理可得BE=CE,$\widehat{BD}$=$\widehat{DC}$,∠BED=90°,根据圆周角定理可得AC⊥CB,根据平行线的判定可得AC∥DO,根据勾股定理可得EO2+BE2=BO2;
(2)首先根据垂径定理可得BE=CE=$\frac{1}{2}$BC=8,然后设⊙O的半径为R,则EO=DO-DE=R-4,利用勾股定理可得方程(R-4)2+82=R2,再解即可.
解答 解:(1)BE=CE,$\widehat{BD}$=$\widehat{DC}$,∠BED=90°,∠BOD=∠A,AC∥DO,AC⊥CB,EO2+BE2=BO2;
(2)∵DO⊥BC,
∴BE=CE=$\frac{1}{2}$BC=8,
设⊙O的半径为R,则EO=DO-DE=R-4,
在Rt△OEB中,由勾股定理得:EO2+BE2=BO2,
即(R-4)2+82=R2,
解得:R=10,
∴⊙O的半径为10.
点评 此题主要考查了垂径定理,以及勾股定理的应用,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:解答题
 如图,正方形网格中每个小正方形边长都是1.
如图,正方形网格中每个小正方形边长都是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
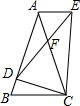 请完成下列的相似测试.
请完成下列的相似测试.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
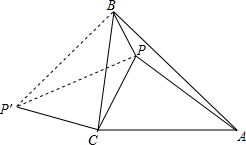 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,且AP=3,CP=2,BP=1,求∠BPC得度数.(提示:把△CAP绕点C逆时针旋转90°到△CBP′,证明△BPP′为Rt△)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com