
【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
A.![]()
B.![]()
C.![]()
D.10﹣5 ![]()
【答案】B
【解析】解:如图,延长BG交CH于点E,
在△ABG和△CDH中,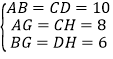 ,
,
∴△ABG≌△CDH(SSS),
AG2+BG2=AB2 ,
∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,
∴∠1+∠2=90°,∠5+∠6=90°,
又∵∠2+∠3=90°,∠4+∠5=90°,
∴∠1=∠3=∠5,∠2=∠4=∠6,
在△ABG和△BCE中, ,
,
∴△ABG≌△BCE(ASA),
∴BE=AG=8,CE=BG=6,∠BEC=∠AGB=90°,
∴GE=BE﹣BG=8﹣6=2,
同理可得HE=2,
在RT△GHE中,GH= ![]() =
= ![]() =2
=2 ![]() ,
,
故选:B.
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,
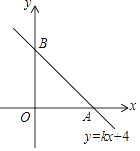
(1)求这条直线的解析式;
(2)若将这条直线沿x轴翻折,求翻折后得到的直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题

(1)公共阅报栏离小红家有______米,小红从家走到公共阅报栏用了______分;
(2)小红在公共阅报栏看新闻一共用了______分;
(3)邮亭离公共阅报栏有______米,小红从公共阅报栏到邮亭用了______分;
(4)小红从邮亭走回家用了______分,平均速度是______米/秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元
万元![]() 其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 | 每公顷获利 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
![]() 求出茄子和西红柿的种植面积各为多少公顷?
求出茄子和西红柿的种植面积各为多少公顷?
![]() 种植场在这一季共获利多少万元?
种植场在这一季共获利多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.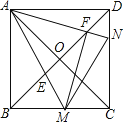
(1)求证: ![]() =
= ![]() ;
;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
【答案】(1) ![]() ;(2)x=
;(2)x=![]()
【解析】试题分析:(1)两边乘以(x-1)(2x+1)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可;
(2)两边乘以(x+2)(x-2)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可.
试题解析:
解:(1)两边乘以(x-1)(2x+1)去分母得:2x+1=5(x-1),
解得:x=2,
当x=2时,(x-1)(2x+1)≠0,
∴原分式方程的解为x=2;
(2)两边乘以(x+2)(x-2)去分母得:(x-2)2-3=(x+2)(x-2),
解得:x=![]() ,
,
当x=![]() 时,(x+2)(x-2)≠0,
时,(x+2)(x-2)≠0,
所以原分式方程的解为x=![]() .
.
【题型】解答题
【结束】
21
【题目】先化简,再求值![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取.
的整数解中选取.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com