
【题目】国庆节期间,南部山区某果园平均每天可卖出 300 斤核桃 ,卖出 1 斤核桃的利润是 1 元,经调查发现,零售单价每降 0.1 元,每天可多卖出 100 斤.设该店决定把零售单价下降 x(0<x<1)元.
(1)零售单价下降 x 元后,该店平均每天可卖出多少斤核桃(用 含出 x 的代数式表示,需要简化);
(2)在不考虑其他国素的条件下,为了薄利多销,当零售单价下降多少时,才能使该店每天获取的利润是 420元?
【答案】(1)(300+1000x);(2)降价 0.4 时,才能使该店每天获取的利润是 420 元并且卖出的核桃更多.
【解析】
(1)零售单价下降 x 元后,每天可多卖出1000x;
(2)卖出 1 斤核桃的利润是 1 元,则单价下降后每天所得利润=单件利润×销量.
解:(1)当零售单价下降 x 元后,可卖出(300+1000x)斤, 故答案为:(300+1000x);
(2)当零售单价下降 x 时,利润为:(1﹣x)(300+100×![]() ),
),
由题意得,(1﹣mx)(300+100×![]() )=420,解得x=0.4或x=0.3,
)=420,解得x=0.4或x=0.3,
则当降价 0.4 时卖出的贺卡更多.
答:降价0.4时,才能使该店每天获取的利润是420元并且卖出的核桃更多.


科目:初中数学 来源: 题型:
【题目】山西省地处中纬度,属于温带大陆性气候,因此适合种植玉米、高粱、大豆、花生等农作物,农民李大叔有一块总面积为![]() 的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:


农作物 | 占地面积( | 产量(千克/垄) | 利润(元/千克) |
玉米 | 30 | 60 | 0.5 |
高粱 | 20 | 50 | 0.8 |
(1)若设高粱种植了![]() 垄,请说明共有几种种植方案,分别是哪几种;
垄,请说明共有几种种植方案,分别是哪几种;
(2)在以上种植方案中,哪种方案获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
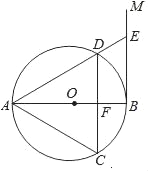
【题目】如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)若AC=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,各边长为 2 的等边三角形有一条 边在同一条直线上,设△B2D1C1 面 积为 S1,△B3D2C2 的面积为 S2,…,△B2019D2018C2018 的面积为 S2018,则 S2018=( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
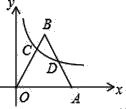
【题目】如图,在平面直角坐标系中,等边三角形OAB的顶点A的坐标为(5,0),顶点B在第一象限,函数y=![]() (x>0)的图象分别交边OA、AB于点C、D.若OC=2AD,则k=_____
(x>0)的图象分别交边OA、AB于点C、D.若OC=2AD,则k=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻AB在阳光下的投影BC=2 m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测量出DE在阳光下的投影长为5 m,请你计算DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料,学校与图书馆的路程是![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线![]() 和线段
和线段![]() 分别表示两人离学校的路程
分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
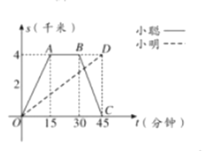
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)求线段![]() 的函数关系式;
的函数关系式;
(4)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com