
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
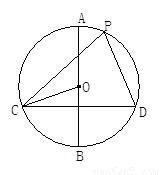
(1)P是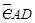 上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.
(1)相等;(2)∠CP′D+∠COB=180°
【解析】
试题分析:(1)连接OD,根据垂径定理可得∠COB=∠DOB,再结合圆周角定理即可得到结果;
(2)连接P′P,则可得∠P′CD=∠P′PD,∠P′PC=∠P′DC.即可得∠P′CD+∠P′DC=∠CPD,从而可以得到结果.
从而∠CP′D+∠COB=180°.
(1)连接OD,
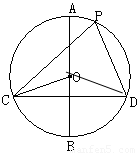
∵AB⊥CD,AB是直径,
∴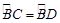 ,
,
∴∠COB= ∠DOB.
∵∠COD=2∠P,
∴∠COB=∠P,即∠COB=∠CPD.
(2)连接P′P,
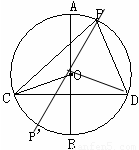
则∠P′CD=∠P′PD,∠P′PC=∠P′DC.
∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.
∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,
从而∠CP′D+∠COB=180°.
考点:垂径定理,圆周角定理
点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| m+n | m-n |
 说明理由;若不成立,请用含m、n的式子表示tan∠DAC.(直接写答案)
说明理由;若不成立,请用含m、n的式子表示tan∠DAC.(直接写答案)查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是
(2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中AB=AC=6cm,BC=8cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.
如图,在△ABC中AB=AC=6cm,BC=8cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com