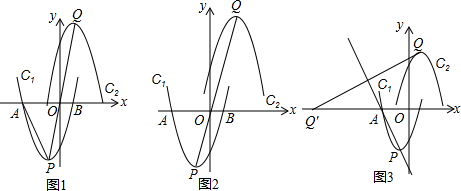
解:(1)∵抛物线C
1:y=(x+1)
2-4的顶点为P,将抛物线C
1关于x轴作轴对称变换,
∴对称图象解析式为:y=-(x+1)
2+4,
∵再将变换后的抛物线沿y轴的正方向、x轴的正方向都平移.m个单位(m>l),得到抛物线C
2,m=3,
∴抛物线C
2的解析式为:y=-(x-2)
2+7;
(2)①∵Q(m-1,m+4),P(-1,-4),PQ被y轴平分,
∴x
Q+x
P=0,
∴m-1=1,
解得:m=2;
②过点P,Q分别作y轴的垂线,垂足分别为:E,F,
∵∠QFO=∠PEO,∠FOQ=∠POE,
∴△OPE∽△OFQ,
∴

=
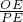
=4,
∴OF=4FQ,
∴m+4=4(m-1),
解得:m=

;
(3)由P(-1,-4),A(-3,0)设直线PA的解析式为y=ax+b,
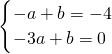
,
解得:
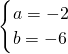
,
∴直线PA的解析式为:y=-2x-6,
∴直线PA与y轴交点为:(0,-6).
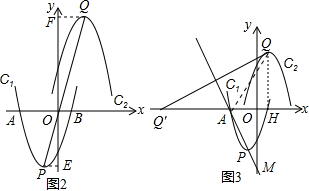
设Q关于PA的对称点为Q′,
则∠QQ′O=∠AMO,
∴tan∠QQ′O=tan∠AMO=
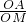
=
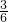
=

,
过Q作QH⊥x轴于H,
则OH=m-1,QH=m+4,Q′H=2m+8,AH=3+(m-1)=m+2,
∴AQ′=2m+8-(m+2)=m+6,
∴AQ=AQ′=m+6,
在Rt△QAH中,AQ
2=AH
2+QH
2,
∴(m+6)
2=(m+2)
2+(m+4)
2,
解得:m
1=-4(舍去),m
2=4.
分析:(1)根据关于x轴对称的抛物线的解析式a,b,c符号相反,进而根据将变换后的抛物线沿y轴的正方向、x轴的正方向都平移3个单位,求出答案即可;
(2)①根据Q(m-1,m+4),P(-1,-4),PQ被y轴平分,得出x
Q+x
P=0,进而求出即可;
②首先得出△OPE∽△OFQ,进而得出

=
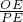
=4,求出即可;
(3)首先求出直线PA的解析式,利用对称性得出tan∠QQ′O=tan∠AMO=
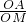
=
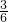
=

,再利用AQ
2=AH
2+QH
2,求出m的值即可.
点评:此题主要考查了二次函数的应用以及勾股定理和锐角三角函数关系以及相似三角形的判定与性质等知识,熟练掌握对称的性质是解题关键.

 =
=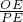 =4,
=4, ;
;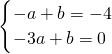 ,
,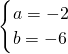 ,
,
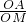 =
=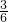 =
= ,
, =
=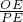 =4,求出即可;
=4,求出即可;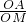 =
=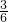 =
= ,再利用AQ2=AH2+QH2,求出m的值即可.
,再利用AQ2=AH2+QH2,求出m的值即可.

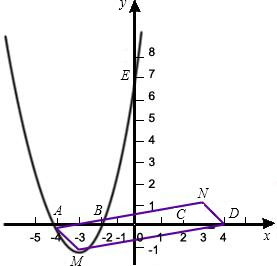 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).