
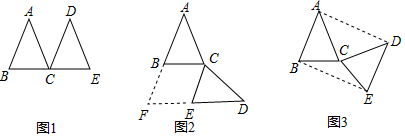
���� ��1����ȫ�ȵó���ABC=��ACB=��DCE=��DEC�������жϳ�BC��DE�����ɵó���ABC=��F�������ó�CE��AB�����ɵó����ۣ�
��2���ɵ��������ε����������ABE=90�㣬ͬ������BAD=��ADE=90�㣬���ɵó����ۣ�
��3���������εó�AB=AD�������ó���ACD�ǵȱ������Σ����������ABC=75�㣮
��� �⣺��1���ı���BCEF�����Σ�
���ɣ��ߡ�ABC�͡�DCE������ȫ�ȵĵ��������Σ�BC��CEΪ�ױߣ�
��BC=CE����ABC=��ACB=��DCE=��DEC��
�ߡ�BCE=��ACB��
���BCE=��DEC��
��BC��DE��
���ABC=��F��
���F=��DEC��
��CE��AB��
���ı���BCEF��ƽ���ı��Σ�
��BC=CE��
��ƽ���ı���BCEF�����Σ�
��2���ߡ�ABC=��ACB����BCE=2��ACB��
���BCE=2��ABC��
��BC=CE��
���CBE=$\frac{1}{2}$��180��-��BCE��=$\frac{1}{2}$��180��-2��ABC��=90��-��ABC��
���CBE+��ABC=90�㣬
���ABE=90�㣬
ͬ������BAD=��ADE=90�㣬
���ı���ABED�Ǿ��Σ�
��3���ı���ABED�ܳ�Ϊ�����Σ�
���ı���ABED�������Σ�
��AB=AD��
��AB=AC=CD��
��AC=AD=CD��
���ACD�ǵȱ������Σ�
���ACD=60�㣬
�ߡ�BCE=2��ACB����ABC=��ACB=��DCE��
���ACB+��BCE+��DCE+��ACD=360�㣬
���ABC+2��ABC+��ABC=300�㣬
���ABC=75�㣬
���� �������ı����ۺ��⣬��Ҫ������ȫ�������ε����ʣ����������ε����ʣ��ȱ������ε��ж������ʣ����ε��ж������ε��ж��������ε����ʣ��⣨1���Ĺؼ��ǵó�BC��DE���⣨2���Ĺؼ����жϳ���ABE=90�㣬�⣨3���Ĺؼ��ǵó���ACD�ǵȱ������Σ���һ���е��Ѷȵ��п������⣮


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
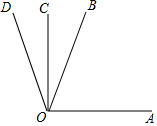 ��AOCΪֱ�ǣ�OC�ǡ�BOD��ƽ���ߣ��ҡ�AOB=57.65�㣬���AOD�Ķ����ǣ�������
��AOCΪֱ�ǣ�OC�ǡ�BOD��ƽ���ߣ��ҡ�AOB=57.65�㣬���AOD�Ķ����ǣ�������| A�� | 122��20�� | B�� | 122��21�� | C�� | 122��22�� | D�� | 122��23�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬PC�С�O��C��AE��PC��PC���ӳ�����E��AE����O��D��PC��AB���ӳ����ཻ�ڵ�P������AC��BC��
��ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬PC�С�O��C��AE��PC��PC���ӳ�����E��AE����O��D��PC��AB���ӳ����ཻ�ڵ�P������AC��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{36}$=��6 | B�� | $\root{3}{-8}$=-$\root{3}{8}$ | C�� | $\sqrt{��-4��^{2}}$=-4 | D�� | -$\sqrt{3.6}$=-0.6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com