
����Ŀ���Ķ�������Լ������ƽ��ֱ������ϵ�У�����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ�ߣ��иõ�ġ������ߡ������磬��M��1��3�����������У�x=1��y=3��y=x+2��y=��x+4��
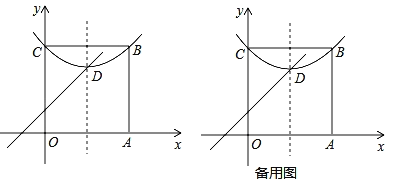
������̽������ͼ����ƽ��ֱ������ϵ����������OABC����B�ڵ�һ���ޣ�A��C�ֱ���x���y���ϣ�������![]() ����B��C���㣬����D���������ڲ���
����B��C���㣬����D���������ڲ���
��1��ֱ��д����D��m��n�����е������ߣ�
��2������D��һ����������y=x+1����������ߵĽ���ʽ��
��3����P��AB���ϳ���A�������һ�㣬����OP������OAP����OP�۵�����A���ڵ�A���λ�ã�����A����ƽ�����������D�����������ʱ�����㣨2��������������������ƽ�ƶ��پ��룬�䶥������OP�ϣ�
���𰸡���1��x=m��y=n��y=x+n��m��y=��x+m+n����2��![]() ����3������������ƽ��
����3������������ƽ��![]() ��
��![]() ���룬�䶥������OP�ϣ�
���룬�䶥������OP�ϣ�
��������
�����������1������������ֱ�������D�������ߣ�
��2���ɵ�D��һ�������ߺ������ε����������D�����꣬�Ӷ���������߽���ʽ��
��2����ƽ����x���y��������������۵������ʼ��㼴�ɣ�
�����������1���ߵ�D��m��n�������D��m��n������������x=m��y=n��y=x+n��m��y=��x+m+n��
��2����D��һ����������y=x+1����n��m=1����n=m+1���������߽���ʽΪ![]() ����
����![]() �����ı���OABC�������Σ���D��Ϊ�����εĶԳ��ᣬD��m��n������B��2m��2m������
�����ı���OABC�������Σ���D��Ϊ�����εĶԳ��ᣬD��m��n������B��2m��2m������![]() ����n=m+1����õ�m=2��n=3��
����n=m+1����õ�m=2��n=3��
��D��2��3�����������߽���ʽΪ![]() ��
��
��3����ͼ������A����ƽ����y���D���������ʱ��
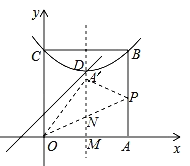
��������ɵã�D��2��3������OA��=OA=4��OM=2�����A��OM=60�㣬���A��OP=��AOP=30�㣬��MN=![]() =
=![]() ������������Ҫ����ƽ�Ƶľ���=
������������Ҫ����ƽ�Ƶľ���=![]() =
=![]() ��
��
��ͼ������A����ƽ����x���D���������ʱ��
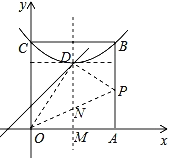
�߶�������OP�ϣ���A����D�غϣ���A�䣨2��3������P��4��c����c��0�������۵��У�PD=PA����![]() ����c=
����c=![]() ����P��4��
����P��4��![]() ������ֱ��OP����ʽΪy=
������ֱ��OP����ʽΪy=![]() ����N��2��
����N��2��![]() ��������������Ҫ����ƽ�Ƶľ���=3��
��������������Ҫ����ƽ�Ƶľ���=3��![]() =
=![]() ����������������ƽ��
����������������ƽ��![]() ��
��![]() ���룬�䶥������OP�ϣ�
���룬�䶥������OP�ϣ�


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶1000��ѧ��������������г�ȡ��300��ѧ���������������ͳ�ƣ����γ�������������ǣ�������
A. 1000��ѧ�� B. ��Уÿ�����꼶ѧ�����������
C. 300 D. �������300��ѧ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD�͡�BDC��ƽ���߽���E��BE��CD�ڵ�F����1+��2=90�㣮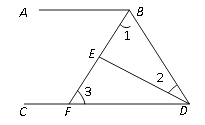
��1����˵����AB��CD��
��2������2=25�㣬���BFC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����dzߵ�����ֱ�Ƕ���O�غ���һ����ͬһƽ������ת����һ�����dzߣ�
��1����ͼ1���� �� B O C = 70�� ���� �� A O D = �� ��
��2����ͼ2���� �� B O C = 50�㣬�� �� A O D = �� ��
��3����ͼ1������� ![]() ��
�� ![]() �Ĺ�ϵ����д�����ɣ�
�Ĺ�ϵ����д�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ��A�س��������������48m,����+48m���������ߡ�32m����Ϊm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в����ж��ı���ABCD��ƽ���ı��ε��ǣ�������
A. AB=CD��AD=BC B. AB��CD��AD=BC
C. AB��CD��AD��BC D. ��A=��C����B=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������2.1ǧ��ѧУ�μӳ��������ᣬ��ѧУʱ�����ݳ��������ڼ��У���ʱ�������Ὺʼ����42���ӣ��������������ٲ��лؼң��ڼ��õ�������1���ӣ�Ȼ���������������г�����ѧУ����֪���������г���ѧУ������ѧУ���е�����ʱ��20���ӣ��������г����ٶ��Dz����ٶȵ�3����
��1���������е��ٶȣ���λ����/�֣��Ƕ��٣�
��2�������ܷ��������Ὺʼǰ�ϵ�ѧУ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������̵�һ���˽�50̨���ԣ��ڶ����˽���32̨���ԣ��������˽�40̨���ԣ��������˽���29̨���ԣ�����˽��������ģ���ô���칲�˽����Զ���̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨����![]() =��a��b����
=��a��b����![]() =��c��d������
=��c��d������![]() =ac+bd����
=ac+bd����![]() =��1��2����
=��1��2����![]() =��3��5������
=��3��5������![]() =1��3+2��5=13��
=1��3+2��5=13��
��1����֪![]() =��2��4����
=��2��4����![]() =��2����3������
=��2����3������![]() ��
��
��2����֪![]() =��x��a��1����
=��x��a��1����![]() =��x��a��x+1������y=
=��x��a��x+1������y=![]() ����y=
����y=![]() �ĺ���ͼ����һ�κ���y=x��1��ͼ���Ƿ��ཻ����˵�����ɣ�
�ĺ���ͼ����һ�κ���y=x��1��ͼ���Ƿ��ཻ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com