练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若三角形三个内角度数的比为2:3:4,则相应的外角比是___________.                   .


    7∶6∶5；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


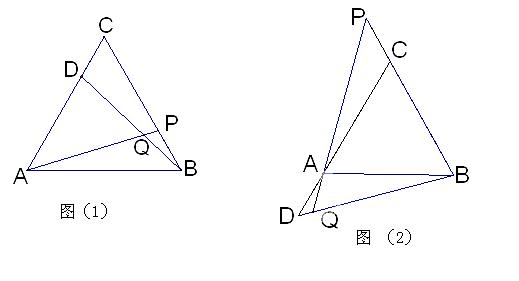
    如图，在等边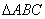的顶点B、C处各有一只蜗牛，它们同时出发，分别以每分钟1个单位的速度由B向C和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D,P处，请问：

    （1）在爬行过程中，BD和AP始终相等吗？为什么？（4分）

    （2）问蜗牛在爬行过程中BD与AP所成的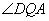的大小有无变化？请证明你的结论。（3分）

    （3）若蜗牛沿着BC和CA的延长线爬行，BD与AP交于点Q，其他条件不变，

    如图（2）所示，蜗牛爬行过程中的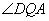大小变化了吗？若无变化，请证

    明。若有变化，请直接写出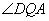的度数。（3分）

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    x=      时，有最小值，最小值是      .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB与CD交于点O，OA＝OC，OD＝OB，∠A=50°，∠B＝30°，则∠D的度数为

    A、50°     B、 30°       C、80°       D、100°

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    把一副常用的三角板如图所示拼在一起，那么图中∠ADE是______度.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，如图，在△ ABC中，AD，AE分别是 △ ABC的高和角平分线，

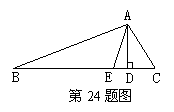    若∠B=30°，∠C=50°.

    （1）求∠DAE的度数。

    （2）试写出 ∠DAE与∠C-∠B有何关系?（不必证明）           

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算结果正确的是（  ）
    A．     B．
    C．     D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


         

    查看答案和解析>>

    科目：初中数学 来源： 题型：


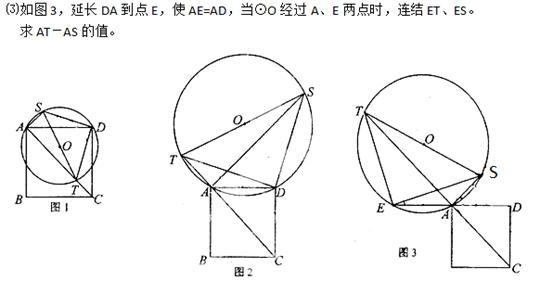
    已知：正方形ABCD的边长为4，⊙O交正方形ABCD的对角线AC所在直线于点T，连接TO交⊙O于点S。

        ⑴如图1，当⊙O经过A、D两点且圆心O在正方形ABCD内部时，连结DT、DS. ①求证：DS=DT,DS⊥DT；  ②求AS+AT的值；

    ⑵如图2，当⊙O经过A、D两点且圆心O在正方形ABCD外部时，连结DT、DS.求AS－AT的值。


    查看答案和解析>>

    同步练习册答案