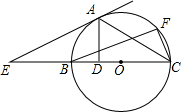
解:(1)在Rt△EOB中EO=

=
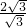
=2,
∴点E的坐标为(-2,0),
在Rt△COA中,OC=OA•tan∠CAO=OA•tan60°=

×

=3,
∴点C的坐标为(-3,0).
(2)∵点C关于对称轴x=-2对称的点的坐标为(-1,0),
点C与点(-1,0)都在抛物线上,
设y=a(x+1)(x+3),把A(0,

)代入得,

=a(0+1)(0+3),
∴a=

,
∴y=

(x+1)(x+3)
即y=

x
2+
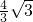
x+

.
(3)⊙M与⊙A外切,
证明如下:∵ME∥y轴,
∴∠MED=∠B,
∵∠B=∠BDA=∠MDE,
∴∠MED=∠MDE,
∴ME=MD,
∵MA=MD+AD=ME+AD,
∴⊙M与⊙A外切.
分析:(1)已知了A点的坐标,即可得出圆的半径和直径,可在直角三角形BOE中,根据∠BEO和OB的长求出OE的长进而可求出E点的坐标,同理可在直角三角形OAC中求出C点的坐标.
(2)已知了对称轴的解析式,可据此求出C点关于对称轴对称的点的坐标,然后根据此点坐标以及C,A的坐标用待定系数法即可求出抛物线的解析式.
(3)两圆应该外切,由于直线DE∥OB,因此∠MED=∠ABD,由于AB=AD,那么∠ADB=∠ABD,将相等的角进行置换后可得出∠MED=∠MDE,即ME=MD,因此两圆的圆心距AM=ME+AD即两圆的半径和,因此两圆外切.
点评:本题着重考查了待定系数法求二次函数解析式、切线的性质、圆与圆的位置关系等知识点.

 )为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD
)为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD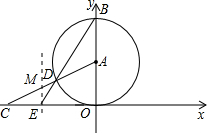 的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C. =
=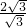 =2,
=2, ×
× =3,
=3, )代入得,
)代入得, =a(0+1)(0+3),
=a(0+1)(0+3), ,
, (x+1)(x+3)
(x+1)(x+3) x2+
x2+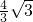 x+
x+ .
.

 名校课堂系列答案
名校课堂系列答案 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.


 D,过A作AE∥BF交CB的延长线于E.
D,过A作AE∥BF交CB的延长线于E. (2012•张家港市模拟)如图,以矩形OABC的顶点O为坐标原点,OA所在的直线为x轴,OC所在的直线为y轴,建立直角坐标系.已知OA=3,OC=2,点E是AB的中点,点F在BC上,CF=1,点M、N分别是x轴、y轴上的动点,则四边形MEFN周长的最小值为
(2012•张家港市模拟)如图,以矩形OABC的顶点O为坐标原点,OA所在的直线为x轴,OC所在的直线为y轴,建立直角坐标系.已知OA=3,OC=2,点E是AB的中点,点F在BC上,CF=1,点M、N分别是x轴、y轴上的动点,则四边形MEFN周长的最小值为