
 £¬µćEŹĒADµÄČżµČ·Öµć£¬ĒŅAE
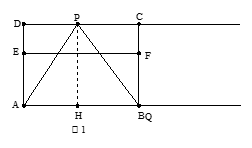
£¬µćEŹĒADµÄČżµČ·Öµć£¬ĒŅAE DE£¬¹żµćE×÷EF”ĪAB½»BCÓŚF£¬²¢×÷ÉäĻßDCŗĶAB£¬µćP”¢Q·Ö±šŹĒÉäĻßDCŗĶÉäĻßABÉĻ¶Æµć£¬µćPŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÓŅĘ½ŅĘ£¬ĒŅŹ¼ÖÕĀś×ć”ĻPQA=60”ć£¬ÉčPµćŌĖ¶ÆµÄŹ±¼äĪŖ
DE£¬¹żµćE×÷EF”ĪAB½»BCÓŚF£¬²¢×÷ÉäĻßDCŗĶAB£¬µćP”¢Q·Ö±šŹĒÉäĻßDCŗĶÉäĻßABÉĻ¶Æµć£¬µćPŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÓŅĘ½ŅĘ£¬ĒŅŹ¼ÖÕĀś×ć”ĻPQA=60”ć£¬ÉčPµćŌĖ¶ÆµÄŹ±¼äĪŖ £®
£®
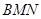 ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öŹ±¼ä
ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öŹ±¼ä µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£® ÓėĖıߊĪ
ÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿ĪŖS£¬ŹŌĒóSÓė
µÄÖŲµž²æ·ÖµÄĆ껿ĪŖS£¬ŹŌĒóSÓė µÄŗÆŹż¹ŲĻµŹ½ŗĶĻąÓ¦µÄ×Ō±äĮæ
µÄŗÆŹż¹ŲĻµŹ½ŗĶĻąÓ¦µÄ×Ō±äĮæ µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®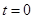 £¬
£¬  £¬
£¬ 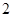 £Ø3£©
£Ø3£©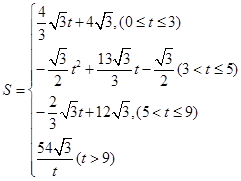
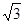 £»
£»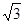 £®
£®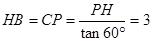 £®
£®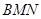 ĪŖµČŃüČż½ĒŠĪ
ĪŖµČŃüČż½ĒŠĪ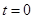 £¬
£¬  £¬
£¬ 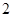 £»
£» ÓėĖıߊĪ
ÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿ĪŖS
µÄÖŲµž²æ·ÖµÄĆ껿ĪŖS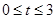 £¬QÓėBµćÖŲŗĻ£¬PµćŌŚCD±ßµÄÖŠµć“¦£¬“ĖŹ±”÷
£¬QÓėBµćÖŲŗĻ£¬PµćŌŚCD±ßµÄÖŠµć“¦£¬“ĖŹ±”÷ ŹĒµČ±ßČż½ĒŠĪ£¬ŌņĖüÓėĖıߊĪ
ŹĒµČ±ßČż½ĒŠĪ£¬ŌņĖüÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿S=
µÄÖŲµž²æ·ÖµÄĆ껿S=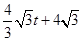 £»µ±
£»µ±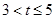 Ź±”÷
Ź±”÷ ÓėĖıߊĪ
ÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿S=
µÄÖŲµž²æ·ÖµÄĆ껿S=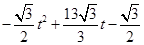 £»µ±
£»µ±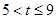 £¬”÷
£¬”÷ ÓėĖıߊĪ
ÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿S=
µÄÖŲµž²æ·ÖµÄĆ껿S=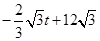 £»µ±
£»µ±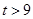 £¬”÷
£¬”÷ ÓėĖıߊĪ
ÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿S=
µÄÖŲµž²æ·ÖµÄĆ껿S=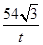 £¬×ŪÉĻĖłŹö”÷
£¬×ŪÉĻĖłŹö”÷ ÓėĖıߊĪ
ÓėĖıߊĪ µÄÖŲµž²æ·ÖµÄĆ껿
µÄÖŲµž²æ·ÖµÄĆ껿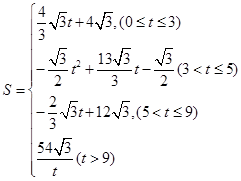



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 µÄĶ¼ĻóĻą½»ÓŚA(£2£¬1)”¢B(1”¢n)Į½µć”£
µÄĶ¼ĻóĻą½»ÓŚA(£2£¬1)”¢B(1”¢n)Į½µć”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 µÄŅ»“ĪŗÆŹż
µÄŅ»“ĪŗÆŹż ŗĶ¶ž“ĪŗÆŹż
ŗĶ¶ž“ĪŗÆŹż .
.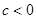 Ź±, ĒóŗÆŹż
Ź±, ĒóŗÆŹż µÄ×ī“óÖµ;
µÄ×ī“óÖµ; ŗĶÅ×ĪļĻß
ŗĶÅ×ĪļĻß ÓŠĒŅÖ»ÓŠŅ»øö¹«¹²µć, Ēó
ÓŠĒŅÖ»ÓŠŅ»øö¹«¹²µć, Ēó µÄÖµ.
µÄÖµ.²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 £Ø·Ö£©±ķŹ¾ĪŚ¹ź“ÓĘšµć³ö·¢ĖłŠŠµÄŹ±¼ä£¬
£Ø·Ö£©±ķŹ¾ĪŚ¹ź“ÓĘšµć³ö·¢ĖłŠŠµÄŹ±¼ä£¬ £ØĆ×£©±ķŹ¾ĶĆ×ÓĖłŠŠµÄĀ·³Ģ£¬
£ØĆ×£©±ķŹ¾ĶĆ×ÓĖłŠŠµÄĀ·³Ģ£¬ £ØĆ×£©±ķŹ¾ĪŚ¹źĖłŠŠµÄĀ·³Ģ£®
£ØĆ×£©±ķŹ¾ĪŚ¹źĖłŠŠµÄĀ·³Ģ£®

 Ӣ
”¢ Ėł±ķŹ¾µÄ
Ėł±ķŹ¾µÄ ”¢
”¢ Óė
Óė Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£» µÄŹµ¼ŹŅāŅ壻
µÄŹµ¼ŹŅāŅ壻 Óė
Óė Ö®¼äµÄŗÆŹż¹ŲĻµµÄĶ¼Ļ󣬲¢Ö±½ÓÅŠ¶ĻĖĻȵ½“ļÖÕµć£»
Ö®¼äµÄŗÆŹż¹ŲĻµµÄĶ¼Ļ󣬲¢Ö±½ÓÅŠ¶ĻĖĻȵ½“ļÖÕµć£»²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 ¶Ö£¬¼×”¢ŅŅĮ½“åŌĖĶłĮ½²ÖæāµÄĄóÖ¦ŌĖŹä·ŃÓĆ·Ö±šĪŖ
¶Ö£¬¼×”¢ŅŅĮ½“åŌĖĶłĮ½²ÖæāµÄĄóÖ¦ŌĖŹä·ŃÓĆ·Ö±šĪŖ ŌŖŗĶ
ŌŖŗĶ ŌŖ£®
ŌŖ£® ”¢
”¢ Óė
Óė Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā


²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
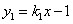 ÓėxÖįÕż°ėÖį½»ÓŚµćA£Ø2£¬0£©£¬ŅŌOAĪŖ±ßŌŚxÖįÉĻ·½×÷Õż·½ŠĪOABC£¬ŃÓ³¤CB½»Ö±Ļß
ÓėxÖįÕż°ėÖį½»ÓŚµćA£Ø2£¬0£©£¬ŅŌOAĪŖ±ßŌŚxÖįÉĻ·½×÷Õż·½ŠĪOABC£¬ŃÓ³¤CB½»Ö±Ļß ÓŚµćD£¬ŌŁŅŌBDĪŖ±ßĻņÉĻ×÷Õż·½ŠĪBDEF£®
ÓŚµćD£¬ŌŁŅŌBDĪŖ±ßĻņÉĻ×÷Õż·½ŠĪBDEF£®
 £¬Čō
£¬Čō £¬ĒóxµÄȔֵ·¶Ī§£®
£¬ĒóxµÄȔֵ·¶Ī§£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗµ„Ń”Ģā
 ²»¾¹ż
²»¾¹ż| A£®µŚŅ»ĻóĻŽ”””” | B£®µŚ¶žĻóĻŽ”” | C£®µŚČżĻóĻŽ”””” | D£®µŚĖÄĻóĻŽ |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com