Question

1．将一副三角尺如图①摆放（在Rt△ABC中，∠ACB=90°，∠B=60°．Rt△DEF中，∠EDF=90°，∠E=45°）．点D为AB的中点，DE交AC于点P，DF经过点C，且BC=2．
（1）求证：△ADC∽△APD；
（2）求△APD的面积；
（3）如图②，将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，试判断$\frac{PM}{CN}$的值是否会随着α的变化而变化，如果不变，请求出$\frac{PM}{CN}$的值；反之，请说明理由．

Answer 1

分析 （1）先判断出△BCD是等边三角形，进而求出∠ADE=∠ACD，即可得出结论；
（2）先用三角函数求出PD，进而求出PH，最后用三角形的面积公式即可得出结论；
（3）只要证明△DPM和△DCN相似，再根据相似三角形对应边成比例即可证明．

解答 （1）证明：由题意知，CD是△ABC中斜边AB上的中线，
∴AD=BD=CD．
∵在△BCD中，BD=CD，且∠B=60°，
∴△BCD为等边三角形．
∴∠BCD=∠BDC=60°，
∴∠ACD=90°-60°=30°，∠ADE=180°-∠BDC-∠EDF=30°，
∴∠ACD=∠ADE=30°，又∵∠A是公共角，
∴△ADC∽△APD．

（2）解：如图①，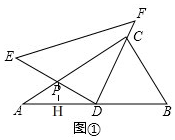

∵△BCD为等边三角形，
∴DC=BC=2．
在Rt△PDC中，∠PCD=30°，
∴PD=DCtan30°=$\frac{2\sqrt{3}}{3}$，
由（1）得∠ADE=30°，
又∠PAD=90°-60°=30°，
∴△PAD是等腰三角形，
∴AP=PD=$\frac{2\sqrt{3}}{3}$，AD=2，
作PH⊥AD于H，
在Rt△PAH中，∠PAH=30°，
∴PH=$\frac{1}{2}$AP=$\frac{1}{2}×\frac{2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$，
S_△PAD=$\frac{1}{2}$AD•PH=$\frac{1}{2}$×$2×\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$．

（3）$\frac{PM}{CN}$的值不会随着α的变化而变化．
∵∠MPD=∠A+∠ADE=60°，
∴∠MPD=∠BCD=60°．
∵在△MPD和△NCD中，∠MPD=∠NCD=60°，∠PDM=∠CDN=α，
∴△MPD∽△NCD，
∴$\frac{PM}{CN}=\frac{PD}{AD}$．
∵在△APD中，∠A=∠ADE=30°，
∴在等腰△APD中，$\frac{PD}{AD}=\frac{\frac{2\sqrt{3}}{3}}{2}$=$\frac{\sqrt{3}}{3}$，
∴$\frac{PM}{CN}=\frac{\sqrt{3}}{3}$．

点评 此题是相似形综合题，主要考查了相似三角形的性质和判定，等边三角形的判定和性质，三角形的面积公式，锐角三角函数，解（1）的关键是得出三角形BCD是等边三角形，解（2）的关键是求出AP的值，解（3）的关键是判断出△MPD∽△NCD．