
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

科目:初中数学 来源: 题型:
【题目】小明家买了一辆小轿车,小明连续记录了某一周每天行驶的路程:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
路程(千米) |
|
|
|
|
|
|
|
请你用学过的知识解决下面的问题:
(1)请你估计小明家的轿车每月(按![]() 天计算)要行驶多少千米?
天计算)要行驶多少千米?
(2)已知每行驶![]() 千米需汽油
千米需汽油![]() 升,汽油每升
升,汽油每升![]() 元,试用含
元,试用含![]() 、
、![]() 的代数式表示小明家每月的汽油费,此代数式为_______;
的代数式表示小明家每月的汽油费,此代数式为_______;
(3)设![]() ,
,![]() ,请你求出小明家一年(按
,请你求出小明家一年(按![]() 个月计算)的汽油费用大约是多少元(精确到千元).(注:第(1)、(3)小题须写出必要步骤)
个月计算)的汽油费用大约是多少元(精确到千元).(注:第(1)、(3)小题须写出必要步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
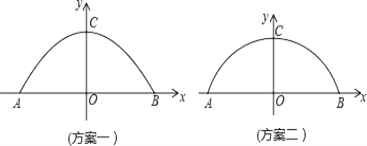
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、D在直线l的同侧.
(1)如图1,在直线l上找一点C.使得线段AC+DC最小(请通过画图指出点C的位置);
(2)如图2,在直线l上取两点B、E,恰好能使△ABC和△DCE均为等边三角形.M、N分别是线段AC、BC上的动点,连结DN交AC于点G,连结EM交CD于点F.
①当点M、N分别是AC、BC的中点时,判断线段EM与DN的数量关系,并说明理由;
②如图3,若点M、N分别从点A和B开始沿AC和BC以相同的速度向点C匀速运动,当M、N与点C重合时运动停止,判断在运动过程中线段GF与直线1的位置关系,并说明理由.
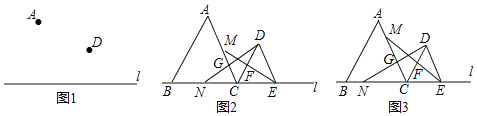
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为_____;
(2)求y关于x的函数关系式,并写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
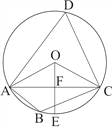
【题目】如图,四边形ABCD 是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC
(1)求∠OCA的度数 (2)如果OE![]() AC于F,且OC=
AC于F,且OC=![]() , 求AC的长
, 求AC的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com