
【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
(1)点D的坐标为 , 点C的坐标为;
(2)若点P是对角线OC上一动点,点E(0,﹣ ![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
【答案】
(1)(1,![]() ),(3,
),(3,![]() );
);
(2)解:作DH⊥x轴于点H,连接DE. 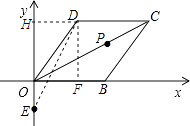
在Rt△OGH中,∠HOG=90°﹣∠DOB=90°﹣60°=30°.
GH=ODsin∠HOG=2× ![]() =1,OH=OGcos∠HOG=2×
=1,OH=OGcos∠HOG=2× ![]() =
= ![]() .
.
则HE=2 ![]() .
.
在直角△HEG中,DE= ![]() .
.
即PE+PB的最小值是 ![]() .
.
【解析】解:(1)作DF⊥OB于点F.
∵B的坐标是(2,0),
∴OB=2,
∴菱形OBCD中,OD=OB=CD=2,
在Rt△ODF中,DF=ODsin∠DOB=2× ![]() =
= ![]() ,OF=ODcos∠DOB=2×
,OF=ODcos∠DOB=2× ![]() =1,
=1,
则D的坐标是(1, ![]() ).
).
则C的坐标是(3, ![]() ).
).
故答案是:(1, ![]() ),(3,
),(3, ![]() );
);
【考点精析】利用勾股定理的概念和菱形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在扇形铁皮AOB中,OA=20,AOB=36°,OB在直线 ![]() 上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第一次落在l上时,停止旋转.则点O所经过的路线长为
上.将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA第一次落在l上时,停止旋转.则点O所经过的路线长为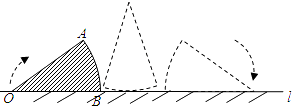 ( )
( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间/(单位:min),然后利用所得数据绘制成如下不完整的统计图表.

根据图表中提供的信息,回答下列问题:
(1)a=_____,b=_____;
(2)将频数分布直方图补充完整;
(3)若该校共1 000名学生,估计有多少学生平均每天的课外阅读时间不少于50min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校兴趣小组,对函数y=|x﹣1|+1的图像和性质进行了研究,探究过程如下:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值如表:
的几组对应值如表:
X | …… |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | …… |
y | …… | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | …… |
其中![]()
(2)在平面直角坐标系中,画出上表中对应值为点的坐标,根据画出的点,画出该函数的图象;

(3)根据画出的函数图像特征,仿照示例,完成下表中函数的变化规律:
序号 | 函数图像特征 | 函数变化规律 |
示例1 | 在直线 | 当 |
① | 在直线 |
|
示例2 | 函数图像经过点(-3,5) | 当 |
② | 函数图像的最低点是 | 当 |
(4)当![]() 时,
时,![]() 的取值范围是_____________
的取值范围是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(﹣1)2018﹣2(π﹣1)0+(﹣![]() )﹣2
)﹣2
(2)(2a﹣4)(![]() a+5)﹣2(a﹣10)
a+5)﹣2(a﹣10)
(3)(2x+3y)(﹣2x+3y)﹣(x﹣3y)2
(4)(4x3y﹣6x2y2+12xy3)÷2xy
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)若CE=12,CF=5,求OC的长;
(2)当点O运动到何处时,四边形AECF是矩形,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.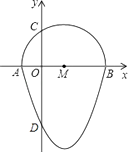
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com