
【题目】∠A=65,∠B=75,将纸片一角折叠,使点C落在△ABC外,若∠2=20,则∠1的度数为 _______.

【答案】100°
【解析】
先根据三角形的内角和定理可出∠C=180°-∠A-∠B=180°-65°-75°=40°;再根据折叠的性质得到∠C′=∠C=40°,再利用三角形的内角和定理以及外角性质得∠3+∠2+∠5+∠C′=180°,∠5=∠4+∠C=∠4+40°,即可得到∠3+∠4=80°,然后利用平角的定义即可求出∠1.
如图,
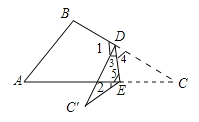
∵∠A=65°,∠B=75°,
∴∠C=180°-∠A-∠B=180°-65°-75°=40°;
又∵将三角形纸片的一角折叠,使点C落在△ABC外,
∴∠C′=∠C=40°,
而∠3+∠2+∠5+∠C′=180°,∠5=∠4+∠C=∠4+40°,∠2=20°,
∴∠3+20°+∠4+40°+40°=180°,
∴∠3+∠4=80°,
∴∠1=180°-80°=100°.
故答案是:100°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

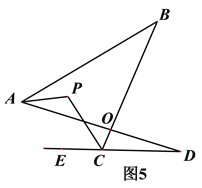
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在2013年义务教育质量监测过程中,为了解学生的家庭教育情况,就八年级学生平时主要和谁在一起生活进行了抽样调查.下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图.

频数分布表
代码 | 和谁一起生活 | 频数 | 频率 |
A | 父母 | 4200 | 0.7 |
B | 爷爷奶奶 | 660 | a |
C | 外公外婆 | 600 | 0.1 |
D | 其它 | b | 0.09 |
合计 | 6000 | 1 |
请根据上述信息,回答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,和外公外婆一起生活的学生所对应扇形圆心角的度数是 ;
(3)若该市八年级学生共有3万人,估计不与父母一起生活的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形OEFG都是正方形,O是正方形ABCD的中心,OE交BC于点M,OG交CD于点N,下列结论:①△ODG≌△OCE;②GD=CE;③OG⊥CE;④若正方形ABCD的边长为2,则四边形OMCN的面积等于1,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的华为P10 plus手机四月售价比三月每台降价500元.如果卖出相同数量的华为P10 plus手机,那么三月销售额为9万元,四月销售额只有8万元.
(1)三月华为P10 plus手机每台售价为多少元?
(2)为了提高利润,该店计划五月购进华为P20 pro手机销售,已知华为P10 plus每台进价为3500元,华为P20 pro每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划六月对华为P10 plus的尾货进行销售,决定在四月售价基础上每售出一台华为P10 plus手机再返还顾客现金![]() 元,而华为P20 pro按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而华为P20 pro按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如,三点坐标分别为A(0,3),B(-3,4),C(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com