
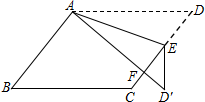
 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度. 分析 由平行四边形的性质得出∠D=∠B=50°,由折叠的性质得:∠D′=∠D=50°,∠EAD′=∠DAE=20°,由三角形的外角性质求出∠AEF=70°,与三角形内角和定理求出∠AED′=110°,即可得出∠FED′的大小.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴∠D=∠B=50°,
由折叠的性质得:∠D′=∠D=50°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=50°+20°=70°,∠AED′=180°-∠EAD′-∠D′=110°,
∴∠FED′=110°-70°=40°;
故答案为:40.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.


科目:初中数学 来源: 题型:解答题
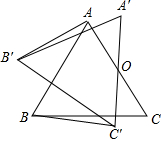 已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.
已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
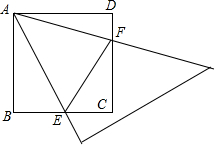 如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品种项目 | 单价(元/棵) | 成活率 |
| A | 80 | 92% |
| B | 100 | 98% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
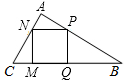 如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.
如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com