
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)
【解答】解:根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)代入上式得:a=![]() ,
,
∴y=![]() (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)=![]() x2﹣
x2﹣![]() x+4=
x+4=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
∴抛物线的对称轴是:x=3;
(2)
P点坐标为(3,![]() ).
).
理由如下:
∵点A(0,4),抛物线的对称轴是x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4)
如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.
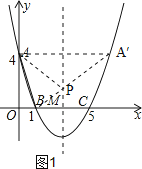
设直线BA′的解析式为y=kx+b,
把A′(6,4),B(1,0)代入得![]() ,
,
解得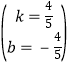 ,
,
∴y=![]() x﹣
x﹣![]() ,
,
∵点P的横坐标为3,
∴y=![]() ×3﹣
×3﹣![]() =
=![]() ,
,
∴P(3,![]() ).
).
(3)
在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
设N点的横坐标为t,此时点N(t,![]() t2﹣
t2﹣![]() t+4)(0<t<5),
t+4)(0<t<5),
如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,
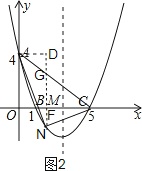
由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣![]() x+4,
x+4,
把x=t代入得:y=﹣![]() t+4,则G(t,﹣
t+4,则G(t,﹣![]() t+4),
t+4),
此时:NG=﹣![]() t+4﹣(
t+4﹣(![]() t2﹣
t2﹣![]() t+4)=﹣
t+4)=﹣![]() t2+4t,
t2+4t,
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CGN=![]() AD×NG+
AD×NG+![]() NG×CF=
NG×CF=![]() NGOC=
NGOC=![]() ×(﹣
×(﹣![]() t2+4t)×5=﹣2t2+10t=﹣2(t﹣
t2+4t)×5=﹣2t2+10t=﹣2(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,△CAN面积的最大值为
时,△CAN面积的最大值为![]() ,
,
由t=![]() ,得:y=
,得:y=![]() t2﹣
t2﹣![]() t+4=﹣3,
t+4=﹣3,
∴N(![]() ,﹣3).
,﹣3).
【解析】(1)抛物线经过点A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解析式为y=a(x﹣1)(x﹣5),代入A(0,4)即可求得函数的解析式,则可求得抛物线的对称轴;
(2)点A关于对称轴的对称点A′的坐标为(6,4),连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小,可求出直线BA′的解析式,即可得出点P的坐标.
(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,![]() t2﹣
t2﹣![]() t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=![]() 的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
(1)求k的值.
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n﹣1,![]() )
)
B.(2n﹣1,![]() )
)
C.(4n+1,![]() )
)
D.(2n+1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传球三次.
(1)请利用树状图列举出三次传球的所有可能情况;
(2)求三次传球后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
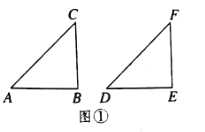
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.
(1)求证:CF=CH;
(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=![]() x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.
求证:四边形ABCD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法和直角三角形全等的判定方法后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情况进行研究.
(初步思考)我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,![]() ,然后,对
,然后,对![]() 进行分类,可分为“
进行分类,可分为“![]() 是直角,钝角,锐角”三种情况进行探索.
是直角,钝角,锐角”三种情况进行探索.
(深入探究)(1)当![]() 是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,
是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,根据 可以知道
,根据 可以知道![]() .
.
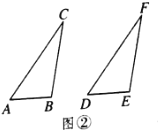
(2)当![]() 是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,
是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,且
,且![]() 都是钝角,求证:
都是钝角,求证:![]() .
.
(3)当![]() 是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,
是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,且
,且![]() 都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)
都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com