
 BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.
BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.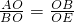 ,∴
,∴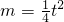 ;
;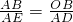 ,其中AB=AD=
,其中AB=AD=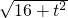 ,AE=m+4,OB=t,∴m=t+
,AE=m+4,OB=t,∴m=t+ -4;
-4;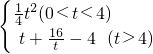 ;
;

科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
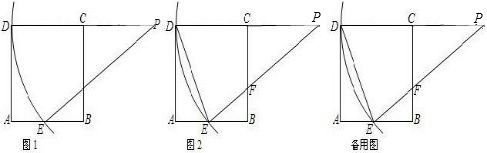
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.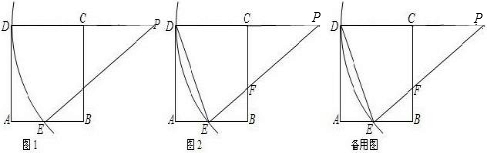
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
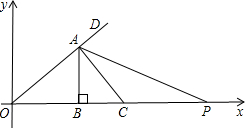
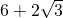 ,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,要求写出计算过程)
,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,要求写出计算过程)
查看答案和解析>>
科目:初中数学 来源:2010年上海市奉贤区中考数学一模试卷(解析版) 题型:解答题
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com