
分析 (1)先计算负整数指数幂、开二次方、零指数幂以及去绝对值,然后根据实数运算顺序进行计算;
(2)先对($\frac{x+2}{x}-\frac{x-1}{x-2}$)$÷\frac{x-4}{{x}^{2}-4x+4}$进行化简、解不等式3x+7>1,然后求值.
解答 (1)解:原式=4-(-1)-3-1+$\sqrt{2}$-1,
=$\sqrt{2}$;
(2)解:原式=$\frac{(x+2)(x-2)-x(x-1)}{x(x-2)}$-$\frac{(x-2)^{2}}{x-4}$,
=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)}$-$\frac{(x-2)^{2}}{x-4}$,
=$\frac{x-4}{x(x-2)}$-$\frac{(x-2)^{2}}{x-4}$,
=$\frac{x-2}{x}$.
由3x+7>1,解得x>-2.
又∵x为负整数,
∴x=-1.
当x=-1时,原式=$\frac{-1-2}{-1}$=3.
点评 本题综合考查了实数的运算、负整数指数幂、零指数幂、二次根式的化简以及分式的化简求值.在分式的化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


科目:初中数学 来源: 题型:解答题
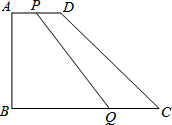 如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB∥DC,∠1=∠B,∠2=∠3.
如图,AB∥DC,∠1=∠B,∠2=∠3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+x-1=0 | B. | x2+1=0 | C. | x2-x+2=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-2且x≠0 | B. | x>-2且x≠0 | C. | x>-2 | D. | x≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )
如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )| A. | 28 | B. | 26 | C. | 25 | D. | 22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com