
【题目】如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣ ![]() x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.
x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.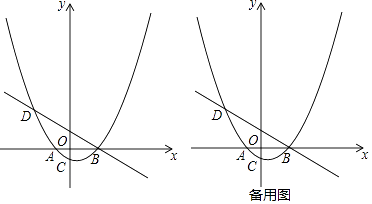
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
【答案】
(1)
解:抛物线y=a(x+2)(x﹣4),令y=0,解得x=﹣2或x=4,
∴A(﹣2,0),B(4,0).
∵直线y=﹣ ![]() x+b经过点B(4,0),
x+b经过点B(4,0),
∴﹣ ![]() ×4+b=0,解得b=
×4+b=0,解得b= ![]() ,
,
∴直线BD解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
当x=﹣5时,y=3 ![]() ,
,
∴D(﹣5,3 ![]() ),
),
∵点D(﹣5,3 ![]() )在抛物线y=a(x+2)(x﹣4)上,
)在抛物线y=a(x+2)(x﹣4)上,
∴a(﹣5+2)(﹣5﹣4)=3 ![]() ,
,
∴a= ![]() .
.
∴抛物线的函数表达式为:y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]()
(2)
解:设P(m, ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() )
)
∴S△BPD= ![]() ×9[(﹣
×9[(﹣ ![]() m+
m+ ![]() )﹣(
)﹣( ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() )]
)]
=﹣ ![]() m2﹣
m2﹣ ![]() m+10
m+10 ![]()
=﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]()
∴△BPD面积的最大值为 ![]()
(3)
解:如图,

作DK∥AB,AH⊥DK,AH交直线BD于点F,
∵由(2)得,DN=3 ![]() ,BN=9,
,BN=9,
∵∠DBA=30°,
∴∠BDH=30°,
∴FG=DF×sin30°= ![]() FD,
FD,
∴当且仅当AH⊥DK时,AF+FH最小,
点M在整个运动中用时为:t=AF+ ![]() FD=AF+FH,
FD=AF+FH,
∵lBD:y=﹣ ![]() x+
x+ ![]() ,
,
∴Fx=Ax=﹣2,F(﹣2,2 ![]() )
)
∴当F坐标为(﹣2,2 ![]() )时,用时最少
)时,用时最少
【解析】(1)首先求出点A、B坐标,然后求出直线BD的解析式,求得点D坐标,代入抛物线解析式,求得a的值;(2)用三角形的面积公式建立函数关系式,再确定出最大值;(3)由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+ ![]() DF.如图,作辅助线,将AF+
DF.如图,作辅助线,将AF+ ![]() DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第2 018个点的坐标为( )
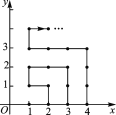
A. (45,9) B. (45,11) C. (45,7) D. (46,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H. 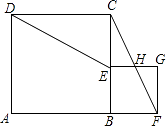
(1)若E是BC的中点,求证:DE=CF;
(2)若∠CDE=30°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 ,中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面内有4个点A(0,2),B(-2,0),C(1,-1),D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.
(3)线段AB,CD有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“智慧南京、绿色出行”,骑共享单车出行已经成为一种时尚.记者随机调查了一些骑共享单车的秦淮区市民,并将他们对各种品牌单车的选择情况绘制成图①和图②的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题: 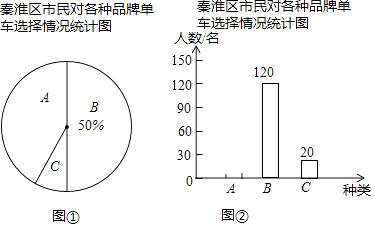
(1)在图①中,C部分所占扇形的圆心角度数为°;
(2)将图②补充完整;
(3)根据抽样调查结果,请你估计某天该区48万名骑共享单车的市民中有多少名选择摩拜单车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com