
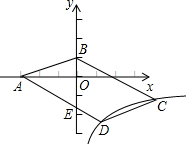
 如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=
如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=| k |
| x |
| 63 |
| 16 |
| 63 |
| 16 |
 解:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,
解:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,| 21 |
| 4 |
| 21 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 4k |
| 9 |
| 21 |
| 4 |
| 4k |
| 9 |
| 21 |
| 4 |
| 4k |
| 9 |
| 63 |
| 16 |
| 63 |
| 16 |


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
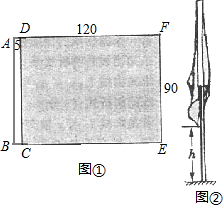 下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.
下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.查看答案和解析>>
科目:初中数学 来源: 题型:
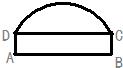 18、如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
18、如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com