Question

【题目】如图，四边形ABCD是正方形，E、F分别是AB和AD延长线上的点，BE＝DF，在此图中是否存在两个全等的三角形，并说明理由；它们能够由其中一个通过旋转而得到另外一个吗？简述旋转过程．

Answer 1

【答案】在此图中存在两个全等的三角形，即△CDF≌△CBE．△CDF是由△CBE绕点C沿顺时针方向旋转90°得到的．理由见解析.

【解析】

在△CDF和△CBE中，根据正方形的性质知DC=BC、已知条件DF=BE可以证得△CDF≌△CBF．

解：在此图中存在两个全等的三角形，即△CDF≌△CBE．理由如下：

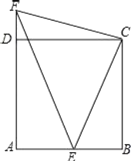
∵点F在正方形ABCD的边AD的延长线上，

∴∠CDF＝∠CDA＝90°；

在△CDF和△CBE中，

，

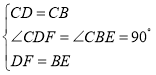∴△CDF≌△CBE（SAS），

∴∠FCD＝∠ECB，CF＝CE，

∴∠FCE＝∠FCD+∠DCE＝∠ECB+∠DCE＝∠DCB＝90°，

∴△CDF是由△CBE绕点C沿顺时针方向旋转90°得到的．