
【题目】如图,完成证明及理由

已知:∠1=∠E,∠B=∠D
求证:AB∥CD
证明:∵ ∠1=∠E( )
∴_______∥_______ ( )
∴ ∠D+∠2=180°( )
∵ ∠B=∠D( )
∴ ∠_______+ ∠_______ = 180°( )
∴ AB∥CD( )
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数。

①若∠ABC=40°,∠ACB=60°,则∠BIC=______°;
②若∠ABC+∠ACB=100°,则∠BIC=___________°;
③若∠A=80°,则∠BIC=_______°;
④从上述计算中,我们能发现已知∠A=x,则∠BIC=_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90°,∠A=75°,点D是AB的中点.将△ACD沿CD翻折得到△A′CD,连接A′B.

(1)求证:CD∥A′B;
(2)若AB=4,求A′B2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D、E分别是斜边AB、直角边BC上的点,把
,D、E分别是斜边AB、直角边BC上的点,把![]() 沿着直线DE折叠.
沿着直线DE折叠.

![]() 如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;
如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;![]() 不写作法和证明,保留作图痕迹
不写作法和证明,保留作图痕迹![]()
![]() 如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于
是关于![]() 的方程
的方程![]() 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形![]() 的两条边长,则
的两条边长,则![]() 的周长为( )
的周长为( )
A. 6 B. 8 C. 10 D. 8或10
查看答案和解析>>
科目:初中数学 来源: 题型:
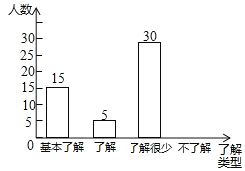
【题目】“校园安全”受到全社会的广泛关注,“高远”中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下尚不完整的条形统计图,且知在抽样调查中“了解很少”的同学占抽样调查人数的![]() ,请你根据提供的信息解答下列问题:
,请你根据提供的信息解答下列问题:
![]() 接受问卷调查的学生共有多少名?
接受问卷调查的学生共有多少名?
![]() 请补全条形统计图;
请补全条形统计图;
![]() 若“高远”中学共有1800名学生,请你估计该校学生对校园知识“基本了解”的有多少名?
若“高远”中学共有1800名学生,请你估计该校学生对校园知识“基本了解”的有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com