
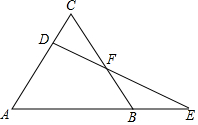
 如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.分析 (1)过D作DM∥AB交BC于M,则△CDM为等边三角形,得CD=DM,而BE=CD,得到DM=BE,易证得△FDM≌△FEB,根据全等三角形的性质即可得到结论;
(2)由(a-5)2+b2-6b+9=0,转化为:(a-5)2+(b-3)2=0,然后根据非负数的性质可得:a=5,b=3,即BC=5,CM=3,求出BM=2,由(1)知△DFM≌△EFB,得出FM=FB=$\frac{1}{2}$BM=1即可.
(3)由(1)得△FDM≌△FEB,得到MF=BF=y,易得CM=CD=x,而BC=5,即有x+y+y=5,即可得到y与x间的函数关系式.
解答 (1)证明:过点D作DM∥AE交BC于点M,
∴∠CDM=∠A,∠CMD=∠ABC,
又∵在等边三角形ABC中,∠A=∠ABC=∠C=60°,
∴∠CDM=∠CMD=∠C ,
,
∴△CDM是等边三角形,
∴CD=DM,
又∵CD=BE,
∴BE=DM,
∵DM∥AE,
∴∠MDF=∠E,
在△DMF和△EBF中,$\left\{\begin{array}{l}{∠MDF=∠E}&{\;}\\{∠DFM=∠EFB}&{\;}\\{DM=BE}&{\;}\end{array}\right.$,
∴△DMF≌△EBF(AAS),
∴DF=EF;
(2)解:∵(a-5)2+b2-6b+9=0,
∴(a-5)2+(b-3)2=0,
∵(a-5)2≥0,(b-3)2≥0,
∴a-5=0,b-3=0,
∴a=5,b=3,
即BC=5,CM=3,
∴BM=2,
∵△DMF≌△EBF,
∴FM=FB=$\frac{1}{2}$BM=1.
(3)解:由(1)得△DMF≌△EBF,
∴BF=MF=y,
由(1)得△CDM是等边三角形,
∴CM=CD=x,
又∵CM+MF+FB=BC=5,
∴2y+x=2,
∴y=-$\frac{1}{2}$x+1(0<x<5).
点评 本题是三角形综合题目,考查了三角形全等的判定与性质.也考查了等边三角形的性质以及一次函数几何图形中的应用;本题综合性强,有一定难度.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
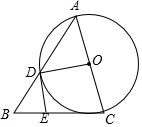 已知:如图,在△ABC中,AC=BC,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
已知:如图,在△ABC中,AC=BC,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
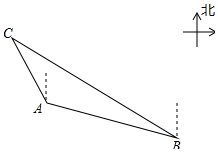 如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号)
如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-5 000=5 000×3.06% | |
| B. | x+5 000×20%=5 000×(1+3.06%) | |
| C. | x+5 000×3.06%×20%=5 000×(1+3.06%) | |
| D. | x+5 000×3.06%×20%=5 000×3.06% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5)、B(-2,1)、C(-1,3)
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5)、B(-2,1)、C(-1,3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com