
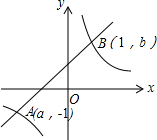 如图,已知反比例函数y=$\frac{2}{x}$与一次函数y=x+1的图象交于点A(a,-1)、B(1,b),则不等式$\frac{2}{x}$≥x+1的解集为x≤-2或0<x≤1.
如图,已知反比例函数y=$\frac{2}{x}$与一次函数y=x+1的图象交于点A(a,-1)、B(1,b),则不等式$\frac{2}{x}$≥x+1的解集为x≤-2或0<x≤1. 分析 先根据函数解析式求得点A的横坐标,再根据函数图象进行判断,双曲线在直线的上方时x的取值范围即为不等式的解集.
解答  解:将A(a,-1)代入一次函数y=x+1,得
解:将A(a,-1)代入一次函数y=x+1,得
-1=a+1,即a=-2
∴A(-2,-1)
当$\frac{2}{x}$≥x+1时,反比例函数值大于或等于一次函数值
根据图象可得,当x≤-2或0<x≤1时,双曲线在直线的上方
∴不等式$\frac{2}{x}$≥x+1的解集为x≤-2或0<x≤1
故答案为:x≤-2或0<x≤1
点评 本题主要考查了反比例函数与一次函数的交点问题.解答此类试题的依据是:①函数图象的交点坐标满足函数解析式;②不等式的解集就是其所对应的函数图象上满足条件的所有点的横坐标的集合.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形纸片ABCD中,CD=12,BC=15,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A1处,求AE的长度.
如图,在矩形纸片ABCD中,CD=12,BC=15,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A1处,求AE的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com