
【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
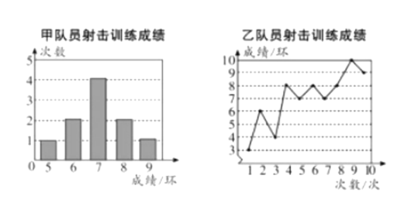
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
【答案】(1)7;7.5;7(2)乙,理由见解析;(3)变小.
【解析】
(1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析;
(3)根据方差公式即可求解判断.
(1)甲的平均成绩a=![]() =7(环),
=7(环),
甲的成绩的众数c=7(环),
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b=![]() =7.5(环),
=7.5(环),
故答案为7;7.5;7
(2)从平均成绩看甲、乙二人的成绩相等均为7环,
从中位数看甲射中7环以上的次数小于乙,
从众数看甲射中7环的次数最多而乙射中8环的次数最多,
从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大;
(3)乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差为:
环,那么乙的射击成绩的方差为:
![]() ×[(37)2+(47)2+(67)2+3×(77)2+3×(87)2+(97)2+(107)2]
×[(37)2+(47)2+(67)2+3×(77)2+3×(87)2+(97)2+(107)2]
=![]() ×(16+9+1+3+4+9)
×(16+9+1+3+4+9)
≈3.8.
故方差变小
故答案为:变小.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
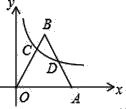
【题目】如图,在平面直角坐标系中,等边三角形OAB的顶点A的坐标为(5,0),顶点B在第一象限,函数y=![]() (x>0)的图象分别交边OA、AB于点C、D.若OC=2AD,则k=_____
(x>0)的图象分别交边OA、AB于点C、D.若OC=2AD,则k=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系 xOy 中,抛物线 y = kx 2 - 2k 2 x -3 交 y 轴于 A 点,交直线 x=-4 于 B 点.
(1)抛物线的对称轴为直线 x=______(用含 k 的代数式表示);
(2)若 AB // x 轴,求抛物线的解析式;
(3)当-4<k<0时,记抛物线在 A,B 之间的部分为图象 G(包含 A,B 两点),若对于图象 G 上任意一点 P( xP , yP ), yP ≥-3 ,结合函数图象写出 k 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料,学校与图书馆的路程是![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线![]() 和线段
和线段![]() 分别表示两人离学校的路程
分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
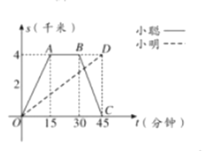
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)求线段![]() 的函数关系式;
的函数关系式;
(4)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
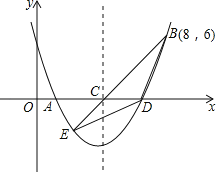
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题发现
如图,![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 经过点
经过点![]() ,与
,与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.

求证:![]() 的周长等于
的周长等于![]() .
.
(1)小明做完该题后,发现![]() 、
、![]() 、
、![]() 存在特定的数量关系,请你直接写出这个数量关系;
存在特定的数量关系,请你直接写出这个数量关系;
拓广探索
(2)如图1,将题中“![]() 平分
平分![]() ”改为“
”改为“![]() 平分
平分![]() 的外角
的外角![]() ”,其他条件不变,请判断
”,其他条件不变,请判断![]() 、
、![]() 、
、![]() 的数量关系,并证明这个数量关系;
的数量关系,并证明这个数量关系;

(3)如图2,将题中“![]() 平分
平分![]() ,
,![]() 平分
平分![]() ”改为“
”改为“![]() 平分
平分![]() 的外角,
的外角,![]() 平分
平分![]() 的外角”,其他条件不变,请直接写出
的外角”,其他条件不变,请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)求出四边形ABPC的面积最大时的P点坐标和四边形ABPC的最大面积;
(3)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com