
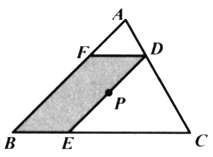
【题目】如图,已知点![]() 是
是![]() 的重心,过
的重心,过![]() 作
作![]() 的平行线
的平行线![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为4,则
的面积为4,则![]() 的面积为______.
的面积为______.
【答案】9
【解析】
延长CP交AB于G.由CP:PG=2:1,推出CE:BC=2:3,AD:AC=1:3,由△CED∽△CBA,△AFD∽△ABC,推出S△CED=![]() ×S△ABC,S△AFD=
×S△ABC,S△AFD=![]() ×S△ABC,由此可得:S平行四边形BEDF=S△ABC-S△CED-S△AFD=
×S△ABC,由此可得:S平行四边形BEDF=S△ABC-S△CED-S△AFD=![]() S△ABC;S△ABC=
S△ABC;S△ABC=![]() S平行四边形BEDF即可解决问题.
S平行四边形BEDF即可解决问题.
解:如图,延长CP交AB于G.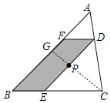
∵点P是△ABC的重心,
∴CP:PG=2:1,
∵DE∥AB,
∴CE:BE=2:1,AD:CD=1:2,
∴CE:CB=2:3,AD:AC=1:3,
∵ED∥AB,DF∥BC,
∴△CED∽△CBA,△AFD∽△ABC,
∴S△CED=![]() ×S△ABC,S△AFD=
×S△ABC,S△AFD=![]() ×S△ABC,
×S△ABC,
∴S平行四边形BEDF=S△ABC-S△CED-S△AFD=![]() S△ABC.
S△ABC.
∴S△ABC=![]() S平行四边形BEDF=
S平行四边形BEDF=![]() ×4=9.
×4=9.


科目:初中数学 来源: 题型:
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
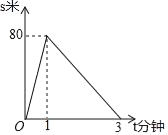
【题目】大课间到了,小明和小欢两人打算从教室匀速跑到600米外的操场做课间操,刚出发时小明就发现鞋带松了,停下来系鞋带,小欢则直接前往操场,小明系好鞋带后立即沿同一路开始追赶小欢,小明在途中追上小欢后继续前行,小明到达操场时课间操还没有开始,于是小明站在操场等待,小欢继续前往操场,设小明和小欢两人想距s(米),小欢行走的时间为t(分钟),s关于t的函数的部分图象如图所示,当两人第三次相距60米时,小明离操场还有_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
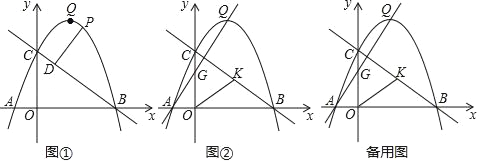
【题目】如图①,已知抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
(1)求直线BC的解析式;
(2)点P是直线BC上方抛物线上的一点,过点P作PD⊥BC于点D,在直线BC上有一动点M,当线段PD最大时,求PM+![]() MB最小值;
MB最小值;
(3)如图②,直线AQ交y轴于G,取线段BC的中点K,连接OK,将△GOK沿直线AQ平移得△G′O'K′,将抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点P(﹣2,1)关于y轴的对称点P′,点T(t,0)是x轴上的一个动点,当△P′TO是等腰三角形时,t的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
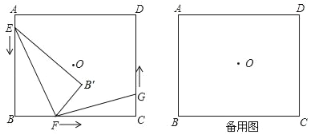
【题目】如图,点O为矩形ABCD的对称中心,AB=5cm,BC=6cm,点E.F.G分别从A.B.C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E.F.G运动的时间为t(单位:s).
(1)当t等于多少s时,四边形EBFB′为正方形;
(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B’与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),……直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1、l2、l3、…、ln分别交于点A1、A2、A3、…、An;函数y=2x的图象与直线l1、l2、l3、…、ln分别交于点B1、B2、B3、…、Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2018=( )
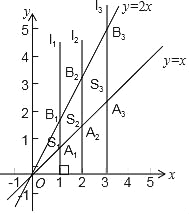
A. 2017.5B. 2018C. 2018.5D. 2019
查看答案和解析>>
科目:初中数学 来源: 题型:
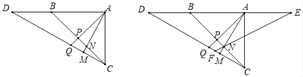
【题目】如图,△ABC中,∠BAC=90°,∠ABC=45°,点D为AB延长线上一点,连接CD,∠AMC=90°,AM交BC于点N,∠APB=90°,AP交CD于点Q.
(1)求证:AN=CQ;
(2)如图,点E在BA的延长线上,且AD=BE,连接EN并延长交CD于点F,求证:DQ=EN;
(3)在(2)的条件下,当3AE=2AB时,请直接写出EN:FN的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com