练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的

    高度CD为100m,点A、D、B在同一直线上,CD⊥AB,则A、B两点的距离是( ）

    A. 200m B. 200m C. m D.

    【答案】D

    【解析】解：∵从热气球C处测得地面A、B两点的俯角分别为30°、45°，∴∠BCD=90°﹣45°=45°，∠ACD=90°﹣30°=60°．∵CD⊥AB，CD=100m，∴△BCD是等腰直角三角形，∴BD=CD=100m．在Rt△ACD中，∵CD=100m，∠ACD=60°，∴AD=CDtan60°=100×=100 m，∴AB=AD+BD=100 +100=100（ +1）m．故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．

    （1）如图1，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；

    （2）如图2，当EF与AB相交时，若∠EAB=α（0°＜α＜90°），请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；

    （3）如图3，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：O是直线AB上的一点，是直角，OE平分．

    （1）如图1．若．求的度数；

    （2）在图1中，，直接写出的度数（用含a的代数式表示）；

    （3）将图1中的绕顶点O顺时针旋转至图2的位置，探究和的度数之间的关系．写出你的结论，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

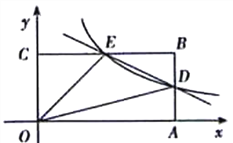
    【题目】如图，在平面直角坐标系中，原点O是矩形OABC的一个顶点，点A、C都

    在坐标轴上，点B的坐标是(4.2)，反比例函数与AB，BC分别交于点D，E。

    (1)求直线DE的解析式；

    (2)若点F为y轴上一点，△OEF和△ODE的面积相等，求点F的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知结论：在直角三角形中，30°所对的直角边是斜边的一半，请利用这个结论进行下列探究活动.如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=，D为AB中点，P为AC上一点，连接PD，把△APD沿PD翻折得到△EPD，连接CE.

    （1）AB=_____,AC=______.

    （2）若P为AC上一动点，且P点从A点出发，沿AC以每秒一单位长度的速度向C运动，设P点运动时间为t秒.

    ①当t=_____秒时，以A、P、E、D、为顶点可以构成平行四边形.

    ②在P点运动过程中，是否存在以B、C、E、D为顶点的四边形是平行四边形？若存在，请求出t的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

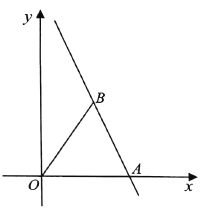
    【题目】如图，直线与轴交于点，点是该直线上一点，满足.

    （1）求点的坐标；

    （2）若点是直线上另外一点，满足，且四边形是平行四边形，试画出符合要求的大致图形，并求出点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学课上，老师出了这样一道题:甲、乙两地相距1400km，乘高铁列车从甲地到乙地比乘特快列车少用9h，已知高铁列车的平均行驶速度是特快列车的2.8倍。求高铁列车从甲地到乙地的时间.老师要求同学先用列表方式分析再解答.下面是两个小组分析时所列的表格:

    小组甲:设特快列车的平均速度为xkm/h.

    小组乙：高铁列车从甲地到乙地的时间为yh

    （1）根据题意，填写表格中空缺的量；（2）结合表格，选择一种方法进行解答.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积可以表示为（ ）

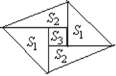
    A. 4S1B. 4S2C. 4S2＋S3D. 2S1＋8S3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

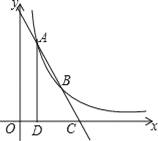
    【题目】如图，点A（1，4）、B（2，a）在函数y=（x＞0）的图象上，直线AB与x轴相交于点C，AD⊥x轴于点D．

    （1）m=　　；

    （2）求点C的坐标；

    （3）在x轴上是否存在点E，使以A、B、E为顶点的三角形与△ACD相似？若存在，求出点E的坐标；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案