
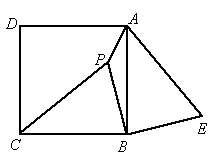
(2005·厦门)已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP,
(1)求证:△CPB≌AEB;
(2)求证PB⊥BE;
(3)若PA∶PB=1∶2,∠APB=135°,求cos∠PAE的值.
|
解法 1 (1)证明∵四边形ABCD是正方形∴BC=AB ∵∠CBP=∠ABE BP=BE ∵△CBP≌△ABE (2)∵证明∠CBP=∠ABE ∴∠PBE=∠ABE+∠ABP=∠CBP+∠ABP=90° ∴PB⊥BE 解法 2(1)、(2)两小题可以一起证明. 证明:∵∠CBP=∠ABE ∴∠PBE=∠ABE+∠ABP=∠CBP+∠ABP=90° ∴PB⊥BE 以B为旋转中心,把△CBP按顺时针方向旋转90°, ∵BC=AB ∠CBA=∠PBE=90° BE=BP ∴△CBP与△ABE重合 ∴△CBP≌△ABE 解 (3)连接PE∵BE=BP ∠PBE=90° ∴∠BPE=45° 设 AP为k,则BP=BE=2k∴ 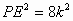 ∴ ∴
∵∠BPA=135° ∠BPE=45° ∴∠APE=90°∴AE=3k 在直角 △APE中: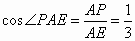 . . |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:022
(2005厦门)已知平面直角坐标系上的三个点O(0,0)、A(-1,1)、B(-1,0),将△ABO绕点O按顺时针方向旋转135°,则点A、B的对应点 、
、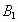 的坐标分别是________.
的坐标分别是________.
查看答案和解析>>
科目:初中数学 来源: 题型:044
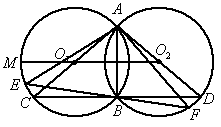
(2005 福建厦门)已知: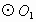 与
与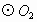 相交于点A、B,过点B作CD⊥AB,分别交
相交于点A、B,过点B作CD⊥AB,分别交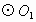 与
与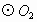 于点C、D.
于点C、D.
(1)如图所示,求证:AC是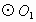 的直径.
的直径.

(2)若AC=AD,
①如图所示,连接 ,求证:四边形是平行四边形;
,求证:四边形是平行四边形;
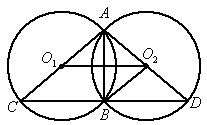
②若点 在
在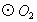 外,延长
外,延长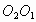 交
交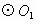 于点M,在劣弧
于点M,在劣弧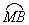 上任取一点E(点E与点B不重合).EB的延长线交优弧
上任取一点E(点E与点B不重合).EB的延长线交优弧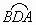 于点F,如图所示.连接AE、AF.则AE________AB(请在横线上填“≥、≤、<、>”这四个不等号中的一个=并加以证明.
于点F,如图所示.连接AE、AF.则AE________AB(请在横线上填“≥、≤、<、>”这四个不等号中的一个=并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com