
【题目】如图,在四边形ABCD中,AB=AC,BC=BD,若![]() ,则
,则![]() ______.(用含
______.(用含![]() 的代数式).
的代数式).

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
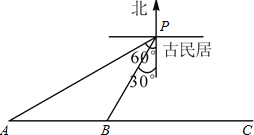
【题目】某市正在进行商业街改造,商业街起点在古民居P的南偏西60°方向上的A处,现已改造至古民居P南偏西30°方向上的B处,A与B相距150m,且B在A的正东方向.为不破坏古民居的风貌,按照有关规定,在古民居周围100m以内不得修建现代化商业街.若工程队继续向正东方向修建200m商业街到C处,则对于从B到C的商业街改造是否违反有关规定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O经过点B,D,E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(1)证明:直线AC是⊙O的切线.
(2)当AE=4,AD=2时,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲车以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙车在甲车出发2小时后匀速前往B地,比甲车早30分钟到达.到达B地后,乙车按原速度返回A地,甲车以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(小时),s与t之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为1小时;③两车在途中第二次相遇时t的值为5.25;④当t=3时,两车相距40千米,其中不正确的个数为( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,以AC为腰在其右侧作△ACD,使AD=AC,连接BD,设∠CAD=.若=60°,CD=2,

(1)求BD的长.
(2)设∠DBC=,请你猜想与的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
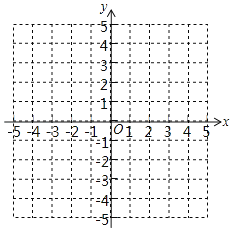
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表填空:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
|
|
| … |
②描点、连线,画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)结合所画函数图象,求方程|x|﹣2x﹣1=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com