
ЁОЬтФПЁПЮЊСЫДДНЈЮФУїГЧЪаЃЌдіЧПбЇЩњЕФЛЗБЃвтЪЖЃЎЫцЛњГщШЁ8УћбЇЩњЃЌЖдЫћУЧЕФРЌЛјЗжРрЭЖЗХЧщПіНјааЕїВщЃЌет8УћбЇЩњЗжБ№БъМЧЮЊ![]() ЃЌЦфжаЁАЁЬЁББэЪОЭЖЗХе§ШЗЃЌЁАЁСЁББэЪОЭЖЗХДэЮѓЃЌЭГМЦЧщПіШчЯТБэЃЎ
ЃЌЦфжаЁАЁЬЁББэЪОЭЖЗХе§ШЗЃЌЁАЁСЁББэЪОЭЖЗХДэЮѓЃЌЭГМЦЧщПіШчЯТБэЃЎ
бЇЩњ РЌЛјРрБ№ |
|
|
|
|
|
|
|
|
ГјгрРЌЛј | ЁЬ | ЁЬ | ЁЬ | ЁЬ | ЁЬ | ЁЬ | ЁЬ | ЁЬ |
ПЩЛиЪеРЌЛј | ЁЬ | ЁС | ЁЬ | ЁС | ЁС | ЁЬ | ЁЬ | ЁЬ |
гаКІРЌЛј | ЁС | ЁЬ | ЁС | ЁЬ | ЁЬ | ЁС | ЁС | ЁЬ |
ЦфЫћРЌЛј | ЁС | ЁЬ | ЁЬ | ЁС | ЁС | ЁЬ | ЁЬ | ЁЬ |
ЃЈ1ЃЉЧѓ8УћбЇЩњжажСЩйгаШ§РрРЌЛјЭЖЗХе§ШЗЕФИХТЪЃЛ
ЃЈ2ЃЉЮЊНјвЛВНСЫНтРЌЛјЗжРрЭЖЗХЧщПіЃЌЯжДг8УћбЇЩњРяЁАгаКІРЌЛјЁБЭЖЗХДэЮѓЕФбЇЩњжаЫцЛњГщШЁСНШЫНгЪмВЩЗУЃЌЪдгУБъМЧЕФзжФИСаОйЫљгаПЩФмГщШЁЕФНсЙћЃЎ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊЕу
ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() .
.
ЃЈ1ЃЉ![]() ЕФЭтНгдВдВаФ
ЕФЭтНгдВдВаФ![]() ЕФзјБъЮЊ .
ЕФзјБъЮЊ .
ЃЈ2ЃЉЂйвдЕу![]() ЮЊЮЛЫЦжааФЃЌдкЭјИёЧјгђФкЛГі
ЮЊЮЛЫЦжааФЃЌдкЭјИёЧјгђФкЛГі![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гы
гы![]() ЮЛЫЦЃЌЧвЕу
ЮЛЫЦЃЌЧвЕу![]() гыЕу
гыЕу![]() ЖдгІЃЌЮЛЫЦБШЮЊ2ЃК1ЃЌЂкЕу
ЖдгІЃЌЮЛЫЦБШЮЊ2ЃК1ЃЌЂкЕу![]() зјБъЮЊ .
зјБъЮЊ .
ЃЈ3ЃЉ![]() ЕФУцЛ§ЮЊ ИіЦНЗНЕЅЮЛ.
ЕФУцЛ§ЮЊ ИіЦНЗНЕЅЮЛ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкAЃЈ2ЃЌ3ЃЉЃЌBЃЈЉ3ЃЌnЃЉСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈ2ЃЌ3ЃЉЃЌBЃЈЉ3ЃЌnЃЉСНЕуЃЎ

ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§BЕузїBCЁЭxжсЃЌДЙзуЮЊCЃЌШєPЪЧЗДБШР§КЏЪ§ЭМЯѓЩЯЕФвЛЕуЃЌСЌНгPCЃЌPBЃЌЧѓЕБЁїPCBЕФУцЛ§ЕШгк5ЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
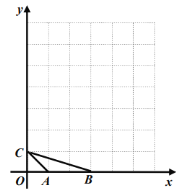
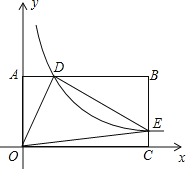
ЁОЬтФПЁПШчЭМЃЌдквдOЮЊдЕуЕФжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФСНБпOCЁЂOAЗжБ№дкxжсЁЂyжсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓгыABЯрНЛгкЕуDЃЌгыBCЯрНЛгкЕуEЃЌШєBDЃН3ADЃЌЧвЁїODEЕФУцЛ§ЮЊ30ЃЌдђkЕФжЕЪЧ_____ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓгыABЯрНЛгкЕуDЃЌгыBCЯрНЛгкЕуEЃЌШєBDЃН3ADЃЌЧвЁїODEЕФУцЛ§ЮЊ30ЃЌдђkЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбвЛИіКЏЪ§ЭМЯѓЩЯУПИіЕуЕФзнзјБъБфЮЊдРДЕФЕЙЪ§ЃЈдКЏЪ§ЭМЯѓЩЯзнзјБъЮЊ0ЕФЕуГ§ЭтЃЉКсзјБъВЛБфЃЌПЩвдЕУЕНСэвЛИіКЏЪ§ЕФЭМЯѓЃЌЮвУЧГЦетИіЙ§ГЬЮЊЕЙЪ§БфЛЛЃЎ
Р§ШчЃКШчЭМ1ЃЌНЋyЃНxЕФЭМЯѓОЙ§ЕЙЪ§БфЛЛКѓПЩЕУЕНyЃН![]() ЕФЭМЯѓЃЎЬиБ№ЕиЃЌвђЮЊyЃНxЭМЯѓЩЯзнзјБъЮЊ0ЕФЕуЪЧдЕуЃЌЫљвдИУЕуВЛзїБфЛЛЃЌвђДЫyЃН
ЕФЭМЯѓЃЎЬиБ№ЕиЃЌвђЮЊyЃНxЭМЯѓЩЯзнзјБъЮЊ0ЕФЕуЪЧдЕуЃЌЫљвдИУЕуВЛзїБфЛЛЃЌвђДЫyЃН![]() ЕФЭМЯѓЩЯвВУЛгазнзјБъЮЊ0ЕФЕуЃЎ
ЕФЭМЯѓЩЯвВУЛгазнзјБъЮЊ0ЕФЕуЃЎ

ЃЈ1ЃЉЧыдкЭМ2жаЛГіyЃНЉxЉ1ЕФЭМЯѓКЭЫќОЙ§ЕЙЪ§БфЛЛКѓЕФЭМЯѓЃЛ
ЃЈ2ЃЉЙлВьЩЯЪіЭМЯѓЃЌНсКЯбЇЙ§ЕФЙигкКЏЪ§ЭМЯѓКЭаджЪЕФжЊЪЖЃЎ
ЂйВТЯыЃКЕЙЪ§БфЛЛЕУЕНЕФЭМЯѓКЭдКЏЪ§ЕФЭМЯѓжЎМфПЩФмгадѕбљЕФСЊЯЕЃПаДГіСНЬѕМДПЩЃЎ
ЂкЫЕРэЃКЧыМђвЊНтЪЭФуЦфжавЛИіВТЯыЃЛ
ЃЈ3ЃЉЩшЭМ2жаЕФЭМЯѓЕФНЛЕуЮЊAЃЌBЃЌШєЕуCЕФзјБъЮЊЃЈЉ1ЃЌmЃЉЃЌЁїABCЕФУцЛ§ЮЊ6ЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋБпГЄЮЊ6cmЕФе§ЗНаЮABCDелЕўЃЌЪЙЕуDТфдкABБпЕФжаЕуEДІЃЌелКлЮЊFHЃЌЕуCТфдкQДІЃЌEQгыBCНЛгкЕуGЃЌЧѓЁїEBGЕФжмГЄЪЧ__________cm.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦћГЕзЈТєЕъОЯњФГжжаЭКХЕФЦћГЕвбжЊИУаЭКХЦћГЕЕФНјМлЮЊ10ЭђдЊ/СОЃЌОЯњвЛЖЮЪБМфКѓЗЂЯжЃКЕБИУаЭКХЦћГЕЪлМлЖЈЮЊ20ЭђдЊ/СОЪБЃЌЦНОљУПжмЪлГі8СОЃЛЪлМлУПНЕЕЭ0.5ЭђдЊЃЌЦНОљУПжмЖрЪлГі1СО
ЃЈ1ЃЉШєУПСОЦћГЕЕФЪлМлНЕЕЭxЭђдЊЃЌдђУПжмЕФЯњЪлСПЪЧЁЁ ЁЁСОЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉШєИУЕъМЦЛЎЦНОљУПжмЕФЯњЪлРћШѓЪЧ90ЭђдЊЃЌЮЊСЫОЁПьМѕЩйПтДцЃЌашНЋУПСОЦћГЕЕФЪлМлНЕЕЭЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНЉx2+4x+5гыyжсНЛгкЕуAЃЌгыxжсЕФе§АыжсНЛгкЕуC.
(1)ЧѓжБЯпACНтЮіЪНЃЛ
(2)Й§ЕуAзїADЦНаагкxжсЃЌНЛХзЮяЯпгкЕуDЃЌЕуFЮЊХзЮяЯпЩЯЕФвЛЕу(ЕуFдкADЩЯЗН)ЃЌзїEFЦНаагкyжсНЛACгкЕуEЃЌЕБЫФБпаЮAFDEЕФУцЛ§зюДѓЪБЃПЧѓЕуFЕФзјБъЃЌВЂЧѓГізюДѓУцЛ§ЃЛ
(3)ШєЖЏЕуPЯШДг(2)жаЕФЕуFГіЗЂбиЪЪЕБЕФТЗОЖдЫЖЏЕНХзЮяЯпЖдГЦжсЩЯЕуMДІЃЌдйбиДЙжБгкyжсЕФЗНЯђдЫЖЏЕНyжсЩЯЕФЕуNДІЃЌШЛКѓбиЪЪЕБЕФТЗОЖдЫЖЏЕНЕуCЭЃжЙЃЌЕБЖЏЕуPЕФдЫЖЏТЗОЖзюЖЬЪБЃЌЧѓЕуNЕФзјБъЃЌВЂЧѓзюЖЬТЗОЖГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпyЃНx2Љ2ax+4a+2ЃЈaЪЧГЃЪ§ЃЉЃЌ
ЃЈЂёЃЉШєИУХзЮяЯпгыxжсЕФвЛИіНЛЕуЮЊЃЈЉ1ЃЌ0ЃЉЃЌЧѓaЕФжЕМАИУХзЮяЯпгыxжсСэвЛНЛЕузјБъЃЛ
ЃЈЂђЃЉВЛТлaШЁКЮЪЕЪ§ЃЌИУХзЮяЯпЖМОЙ§ЖЈЕуHЃЎ
ЂйЧѓЕуHЕФзјБъЃЛ
ЂкжЄУїЕуHЪЧЫљгаХзЮяЯпЖЅЕужазнзјБъзюДѓЕФЕуЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com