
【题目】如图1,经过原点O的抛物线![]() 与x轴交于另一点
与x轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
![]() 求这条抛物线的表达式;
求这条抛物线的表达式;
![]() 在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
![]() 如图2,若点M在这条抛物线上,且
如图2,若点M在这条抛物线上,且![]() ,
,
![]() 求点M的坐标;
求点M的坐标;
![]() 在
在![]() 的条件下,是否存在点P,使得
的条件下,是否存在点P,使得![]() ∽
∽![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]() 存在满足条件的点P,其坐标为
存在满足条件的点P,其坐标为![]() 或
或![]()
【解析】
![]() 由直线解析式可求得B点坐标,由A、B坐标,利用待定系数法可求得抛物线的表达式;
由直线解析式可求得B点坐标,由A、B坐标,利用待定系数法可求得抛物线的表达式;
![]() 过C作
过C作![]() 轴,交x轴于点E,交OB于点D,过B作
轴,交x轴于点E,交OB于点D,过B作![]() 于点F,可设出C点坐标,利用C点坐标可表示出CD的长,从而可表示出
于点F,可设出C点坐标,利用C点坐标可表示出CD的长,从而可表示出![]() 的面积,由条件可得到关于C点坐标的方程,可求得C点坐标;
的面积,由条件可得到关于C点坐标的方程,可求得C点坐标;
(3)①设MB交y轴于点N,则可证得![]() ≌
≌![]() ,可求得N点坐标,可求得直线BN的解析式,联立直线BM与抛物线解析式可求得M点坐标;
,可求得N点坐标,可求得直线BN的解析式,联立直线BM与抛物线解析式可求得M点坐标;
②过M作![]() 轴于点G,由B、C的坐标可求得OB和OC的长,由相似三角形的性质可求得
轴于点G,由B、C的坐标可求得OB和OC的长,由相似三角形的性质可求得![]() 的值,当点P在第一象限内时,过P作
的值,当点P在第一象限内时,过P作![]() 轴于点H,由条件可证得
轴于点H,由条件可证得![]() ∽
∽![]() ,由
,由![]() 的值,可求得PH和OH,可求得P点坐标;当P点在第三象限时,同理可求得P点坐标.
的值,可求得PH和OH,可求得P点坐标;当P点在第三象限时,同理可求得P点坐标.
解:![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
把A、B两点坐标代入抛物线解析式可得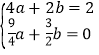 ,
,
解得![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
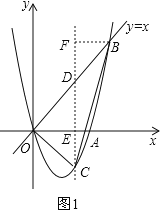
![]() 如图1,过C作
如图1,过C作![]() 轴,交x轴于点E,交OB于点D,过B作
轴,交x轴于点E,交OB于点D,过B作![]() 于点F,
于点F,
![]() 点C是抛物线上第四象限的点,
点C是抛物线上第四象限的点,
![]() 可设
可设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
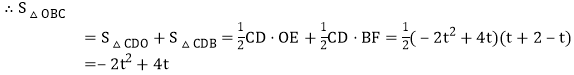 ,
,
![]() 的面积为2,
的面积为2,
![]() ,解得
,解得![]() ,
,
![]() ;
;
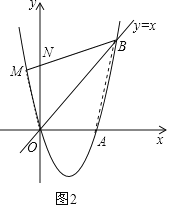
(3)①设MB交y轴于点N,如图2,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
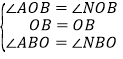 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() 可设直线BN解析式为
可设直线BN解析式为![]() ,
,
把B点坐标代入可得![]() ,解得
,解得![]() ,
,
![]() 直线BN的解析式为
直线BN的解析式为![]() ,
,
联立直线BN和抛物线解析式可得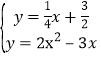 ,
,
解得![]() 或
或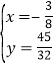 ,
,
![]() ,
,
②![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,![]() ,
,
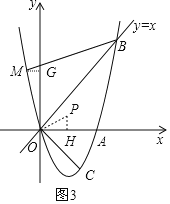
当点P在第一象限时,如图3,过M作![]() 轴于点G,过P作
轴于点G,过P作![]() 轴于点H,
轴于点H,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
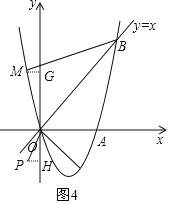
当点P在第三象限时,如图4,过M作![]() 轴于点G,过P作
轴于点G,过P作![]() 轴于点H,
轴于点H,
同理可求得![]() ,
,![]() ,
,
![]() ;
;
综上可知存在满足条件的点P,其坐标为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:∠A=90°,∠ABD=60°,∠CBD=54°,AB=200 m,BC=300 m.请你计算出这片水田的面积.(参考数据:sin 54°≈0.809,cos 54°≈0.588,tan 54°≈1.376,![]() =1.732)
=1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,CD为AB边上中线,E是CB边上的一个动点.
,CD为AB边上中线,E是CB边上的一个动点.
![]() Ⅰ
Ⅰ![]() 求CD的长;
求CD的长;
![]() Ⅱ
Ⅱ![]() 如图1,连接AE,交CD于点F,当AE平分
如图1,连接AE,交CD于点F,当AE平分![]() 时,求CE,CF的长;
时,求CE,CF的长;
![]() Ⅲ
Ⅲ![]() 如图2,连接DE,将
如图2,连接DE,将![]() 沿DE翻折至
沿DE翻折至![]() ,连接BG,直接写出
,连接BG,直接写出![]() 和
和![]() 间的数量关系.
间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,AB是![]() 的直径,且
的直径,且![]() ,点M为
,点M为![]() 外一点,且MA,MC分别切
外一点,且MA,MC分别切![]() 于点A、C两点
于点A、C两点![]() 与AM的延长线交于点D.
与AM的延长线交于点D.
![]() 求证:
求证:![]() ;
;
![]() 填空
填空
![]() 当
当![]() ______时,四边形AOCM是正方形.
______时,四边形AOCM是正方形.
![]() 当
当![]() ______时,
______时,![]() 为等边三角形.
为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(问题情境)
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?


(探索新知)
从面积的角度思考,不难发现:大正方形的面积=小正方形的面积 + 4个直角三角形的面积,从而得数学等式: ;(用含字母a、b、c的式子表示)化简证得勾股定理:![]()
(初步运用)
(1)如图1,若b=2a ,则小正方形面积:大正方形面积= ;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a= 4,b= 6此时空白部分的面积为 ;
(迁移运用)
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?带着这个疑问,小丽拼出图3的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
知识补充:如图4,含60°的直角三角形,对边y :斜边x=定值k
查看答案和解析>>
科目:初中数学 来源: 题型:
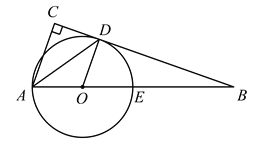
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,![]() ,
,![]() ,
,![]() 绕点C旋转,角的两边分别与AB、AD交于点E、F,同时也分别与DA、BA的延长线交于点G、H.
绕点C旋转,角的两边分别与AB、AD交于点E、F,同时也分别与DA、BA的延长线交于点G、H.
![]() 如图1,若
如图1,若![]() .
.
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 在
在![]() 绕点C旋转的过程中,线段AC、AG、AH之间存在着怎样的数量关系?并说明理由.
绕点C旋转的过程中,线段AC、AG、AH之间存在着怎样的数量关系?并说明理由.
![]() 如图2,若
如图2,若![]() ,经探究得
,经探究得![]() 的值为常数k,求k的值.
的值为常数k,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com