练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．下列计算正确的是（　　）
    A．$\sqrt{8}-\sqrt{2}=\sqrt{2}$B．（-3）2=6C．3a4-2a2=a2D．（-a3）2=a5

    分析 根据实数的运算法则以及整式的运算法则即可判断

    解答 解：（A）原式=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$，故A正确，
    （B）原式=9，故B错误；
    （C）3a4与2a2不是同类项，故C错误；
    （D）原式=a6，故D错误；
    故选（A）

    点评 本题考查学生的运算能力，解题的关键是熟练运用运算法则，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

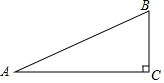    17．如图，在△ABC中，∠C=90°，BC=5，AB=13，则sinB是（　　）
    A．$\frac{5}{13}$B．$\frac{5}{12}$C．$\frac{12}{13}$D．$\frac{13}{12}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列命题中是真命题的是（　　）
    A．经过直线外一点，有且仅有一条直线与一线与已知直线垂直
    B．平分弦的直径垂直于弦
    C．对角线互相平分且垂直的四边形是菱形
    D．反比例函数y=$\frac{k}{x}$，当k＜0时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

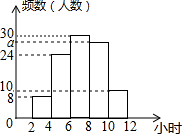    15．某校为了解清明假期全校同学参加课外活动的情况，抽查了100名同学，统计它们假期参加课外活动的时间并绘成频数分布直方图（如图），则参加课外活动时间的中位数所在的范围是（　　）
    A．4-6小时B．6-8小时C．8-10小时D．10-12小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

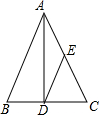    2．如图，△ABC中，AB=AC=15，AD平分∠BAC，点E为AC的中点，连接DE，若△CDE的周长为21，则BC的长为（　　）
    A．16B．14C．12D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．问题背景：已知在△ABC中，边AB上的动点D由A向B运动（与A，B不重合），同时点E由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于点F，点H是线段AF上一点，求$\frac{AC}{HF}$的值．
    （1）初步尝试     如图（1），若△ABC是等边三角形，DH⊥AC，且点D、E的运动速度相等，小王同学发现可以过点D作DG∥BC交AC于点G，先证GH=AH，再证GF=CF，
    从而求得$\frac{AC}{HF}$的值为2．
    （2）类比探究
    如图（2），若△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是$\sqrt{3}$：1，求$\frac{AC}{HF}$的值．
    （3）延伸拓展
    如图（3）若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记$\frac{BC}{AC}$=m，且点D、E的运动速度相等，试用含m的代数式表示$\frac{AC}{HF}$的值（直接写出果，不必写解答过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．tan30°的值为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．在下列调查中，适宜采用普查的是（　　）
    A．了解我省中学生的视力情况B．了解八（1）班学生校服的尺码情况
    C．检测一批炮弹的杀伤半径D．调查电视剧《人民的名义》的收视率

    查看答案和解析>>

    同步练习册答案